克服机器学习转换器的局限性——从位置嵌入到RoPE和ALiBi方法 原创

本文将从早期的正弦算法跟踪分析到当前最新的RoPE和ALiBi算法，介绍如何通过先进的位置编码来克服LLM开发中转换器的局限性。

引言

近年来开发出的机器学习模型的指数级进步与转换器架构的出现密切相关。以前，人工智能科学家必须先为手头的每项任务选择架构，然后再进行超参数优化以获得最佳性能。限制科学家们潜力的另一个挑战是难以处理数据的长期依赖性，难以解决梯度消失、长序列上下文丢失以及因局部约束而无法捕获全局上下文的问题。此外，传统模型缺乏可扩展性和并行性，减缓了对大型数据集的训练，最终阻碍了该领域的进展。

转换器架构通过其自我注意机制解决了这些问题，从而彻底改变了该领域。它使模型能够捕获长序列上的关系，并有效地理解全局上下文，同时具有高度的并行性和跨各种模态如文本、图像等的适应性。在自我注意力机制中，对于每个标记，将其查询与所有其他标记的键进行比较，以计算相似性得分。然后，这些相似性被用来衡量值向量，最终决定当前标记应关注的位置。自我注意将所有标记视为同等重要，无论其顺序如何，失去了关于标记出现顺序的关键信息；换句话说，它将输入数据视为一个没有顺序的集合。

现在，我们需要一种机制来对数据强制执行一些顺序概念，因为自然语言和许多其他类型的数据本质上是顺序和位置敏感的。这就是位置嵌入发挥作用的地方。位置嵌入对序列中每个标记的位置进行编码，使模型能够保持对序列结构的感知。在粗略了解了各种编码位置信息的方法后，接下来我们将详细地对它们展开逐一介绍。

基于DALL-E模型生成的图像

注意机制

设S={w_i}，对于i=1，…，N是N个输入标记的序列，其中w_i表示第i个标记。因此，对于i＝1，…，N，S的相应标记嵌入可以表示为E＝｛x_i｝，其中x_i是标记w_i的d维标记嵌入向量。自我注意机制将位置嵌入结合到标记嵌入中，并生成查询、键和值表示，如下所示：

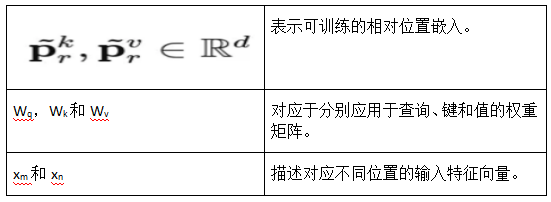
q_m，k_n和v_n：分别代表与序列中第m-th和n-th位置对应的查询、键和值向量；

f_q，f_k和f_v：这些函数把位置信息嵌入到输入嵌入x_m和x_n中，以便生成查询、键和值向量。

然后，根据查询和关键向量之间的相似性计算注意力权重：

注意，权重决定了标记n对标记m的重要性。换句话说，标记m应该对标记n给予多少注意。标记m的输出是作为值向量的加权和计算的：

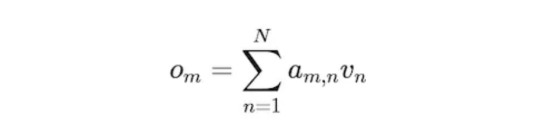
因此，注意机制标记m从序列中的其他标记收集信息。

图1：转换器架构中的位置编码（图片来自论文https://arxiv.org/pdf/1706.03762）。

1.绝对位置嵌入

方程式（1）的典型选择是：

其中p_i是d维向量，表示标记x_i的绝对位置。正弦位置编码和学习位置编码是生成p_i的两种替代方案。

（1）a正弦位置编码

正弦位置编码是在提出转换器架构的​​《Attention is all you need》​​论文中引入的。正弦位置编码为输入序列中的每个标记提供唯一的位置表示。它基于不同频率的正弦和余弦函数，如下所示：

其中，pos是标记在序列中的位置，d是位置嵌入维度，i是维度索引（0<=i<d）。

正弦和余弦函数在正弦位置编码中的使用与傅里叶变换有着密切的关系。通过使用一系列不同的频率对位置进行编码，转换器创建了一个类似于傅里叶变换的表示，其中：

• 高频分量（较低的i）使模型能够捕获本地位置信息。这对于理解序列中相邻标记（如单词对）之间的关系非常有用。
• 低频分量（i值越高）在整个序列中捕获了更多的全局模式。这有助于模型关注可能相距甚远的标记之间更广泛的关系，例如两个不同句子中单词之间的依赖关系。

这有助于模型通过比较标记的位置编码来理解标记的相对位置。正弦位置编码在推理时推广到更大的序列长度时不需要额外的训练参数。然而，它的表现力是有限的。

（2）b学习位置编码

《Attention is all you need》论文中介绍了学习位置编码，并将其应用于BERT和GPT模型中，作为正弦位置编码的替代方案。在学习位置编码中，序列中的每个位置（例如第一个标记、第二个标记等）都被分配了一个嵌入向量。这些位置嵌入是在训练过程中与其他转换器参数一起学习的。例如，如果模型的上下文长度为512，标记嵌入大小为768（即d=768），则大小为512*768的可学习张量将被添加到其他可训练参数中。这意味着，模型会逐渐学习为特定任务（如文本分类或翻译）编码位置信息的最佳方法。

学习位置嵌入比正弦位置嵌入更具表现力，因为模型可以学习位置嵌入，对其特定任务有效。然而，它们引入了更多可训练的参数，这增加了模型的大小及其计算成本。

2.相对位置嵌入

正弦和学习位置编码都侧重于标记的绝对位置。然而，注意力机制是通过计算序列中每个特定标记的其他标记的重要性来工作的。因此，这个过程取决于标记的相对位置（它们彼此相距多远），而不是标记的绝对位置。为了解决绝对位置嵌入的局限性，引入了相对位置编码。

​​RelativePosEmb​​不会将位置信息添加到标记嵌入中。相反，它修改了在每一层计算键和值的方式，如下所示：

上面公式中：

这里，r=clip（m-n，R_min，R_max）表示位置m和n之间的相对距离。假设精确的相对位置在一定距离之外没有用，则对最大相对位置进行剪裁。剪切最大距离使模型能够在推理时进行外推，即推广到训练期间没有看到的序列长度。然而，这种方法可能会从标记的绝对位置（如第一个标记的位置）中遗漏一些有用的信息。

你可能会注意到f_q缺少位置嵌入。这是因为我们正在对相对位置进行编码。在注意力公式中，查询和键值用于计算注意力权重，如方程（2）所示；因此，我们只需要查询或键包含相对位置嵌入即可。

当前，这种编码已被用于许多模型，如​​转换器XL​​和​​T5​​。在参考文献【​​7​​】和【​​8​​】中可以找到应用相对位置编码的不同替代方案。

3.旋转位置嵌入（RoPE）

与之前的方法不同，RoPE根据标记的位置在多维空间中旋转向量。它没有将位置信息添加到标记嵌入中，而是将每一层的注意力权重计算方式修改为：

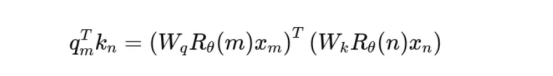
上面公式中：

• W_q，W_k：分别表示查询和键权重矩阵；_​
• R_θ(m)和R_θ(n)：分别表示编码位置m和位置n的标记的绝对位置的旋转矩阵；
• xm和xn：分别表示位置m和位置n的标记嵌入；
• θ：是一个控制位置旋转速率的常数。

这种算法提出了一个广义旋转矩阵，适用于任何偶数嵌入维数d，如下所示：

其中θ_i是预定义的：

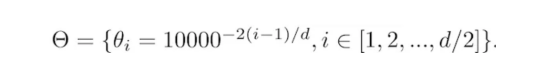
将RoPE（https://arxiv.org/pdf/2104.09864）应用于注意力权重将得到如下公式：

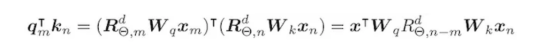
请注意，RoPE公式不会将位置信息添加到注意力模块的值中。注意力模块的输出是值向量的加权和，由于位置信息没有添加到值中，因此每个转换器层的输出都没有明确的位置细节。

​​LLaMA​​和​​GPT-NeoX​​等流行模型也正在使用RoPE。

图2：​​ALiBi方法​​可视化（图片来自论文https://arxiv.org/pdf/2108.12409）。

4.注意线性偏差（ALiBi）

​​ALiBi算法​​也不会在单词嵌入中添加位置编码；相反，它对注意力权重分数增加了一个惩罚，该惩罚与标记之间的距离成正比。因此，每层两个标记i和j之间的注意力得分计算如下：

注意力得分=query_i ×key_j-m ×（i-j）

其中，-m ×（i-j）是一个惩罚值，与标记i和j之间的距离成正比。标量m是训练前固定的头部特定斜率，其不同头部的值被选择为几何序列。例如，对于头部值8，m可能是：

这意味着，第一个头部有一个相对较大的m，因此它更多地惩罚相距较远的标记，并专注于最近的标记，而第八个头有最小的m，使其能够处理更远的标记。前面的图2还提供了相应的可视化表示。

当前，ALiBi算法已经应用于​​BloombergGPT模型​​和​​BLOOM模型​​。

推理时的转换器外推

推理时的转换器外推是指模型能够很好地处理比训练时更长的输入序列。转换器机制与输入长度无关，这意味着在推理时，它可以处理更长的序列。然而，请注意，计算成本随输入长度呈二次方增长，即使转换器层本身与之无关。

ALiBi的作者证明了转换器外推的瓶颈是它的位置嵌入方法。如图3所示，他们比较了不同位置嵌入方法的外推能力。由于学习位置嵌入不能对大于训练长度的位置进行编码，因此它没有外推能力。

图3：外推法：随着输入序列变长（x轴），正弦、RoPE和T5位置编码显示出困惑度降低（在y轴上，越低越好），而ALiBi则没有（图片来自​​论文​​）。

图3显示出，正弦位置嵌入在实践中的外推能力非常有限。虽然RoPE算法的性能优于正弦曲线算法，但它仍然没有达到令人满意的结果。T5偏置方法（相对位置嵌入的一种形式）比正弦算法和RoPE算法嵌入具有更好的外推效果。不幸的是，T5算法偏差的计算成本很高（图4）。ALiBi算法的性能优于所有这些位置嵌入，内存增加则可以忽略不计（0-0.7%）。

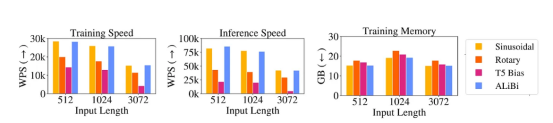
图4：正弦、RoPE、T5和ALiBi算法位置编码的批处理训练、推理速度和内存使用的比较（图片来自​​论文​​）

结论

总之，转换器架构中位置信息的编码方式会显著影响其理解顺序数据的能力，尤其是在推理时的外推时。虽然绝对位置嵌入方法提供了位置感知，但它们经常难以进行转换器外推。这就是为什么提出了更新的位置嵌入。相对位置编码算法RoPE和ALiBi算法具有在推理时进行外推的能力。最后，随着转换器在各种应用中的不断集成，完善位置编码对于突破其性能极限具有非常重要的意义。

注意：本中表达的意见仅代表我们自己的观点。

参考文献

【1】Vaswani, A. “Attention is all you need.” (2017)。

【2】​​BERT​​：Devlin, Jacob，“Bert: Pre-training of deep bidirectional transformers for language understanding”（2018）。

【3】​​GPT​​：Radford, Alec等，“Language models are unsupervised multitask learners.”（2019）。

【4】​​RelativePosEmb​​：Shaw, Peter等，“Self-attention with relative position representations.”（2018）。

【5】​​Transformer-XL​​Dai, Zihang，“Transformer-xl：Attentive language models beyond a fixed-length context.”（2019）。

【6】​​T5​​：Raffel, Colin等，“Exploring the limits of transfer learning with a unified text-to-text transformer.” （2020）。

【7】Raffel, Colin等，“Exploring the limits of transfer learning with a unified text-to-text transformer.”（2020）。

【8】He, Pengcheng等，“Deberta：Decoding-enhanced bert with disentangled attention.”（2020）。

【9】​​RoPE​​：Su, Jianlin等，“Roformer: Enhanced transformer with rotary position embedding.”（2024）。

【10】​​LLaMA​​：Touvron, Hugo等，“Llama: Open and efficient foundation language models.”（2023）。

【11】​​GPT-NeoX​​：Black, Sid等，“Gpt-neox-20b: An open-source autoregressive language model.”（2022）。

【12】​​ALiBi​​：Press, Ofir等，“Train short, test long: Attention with linear biases enables input length extrapolation.”（2021）。

【13】​​BloombergGPT​​：Wu, Shijie等，“Bloomberggpt: A large language model for finance.”（2023）。

【14】​​BLOOM​​：Le Scao, Teven等，“Bloom: A 176b-parameter open-access multilingual language model.”（2023）。

译者介绍

朱先忠，51CTO社区编辑，51CTO专家博客、讲师，潍坊一所高校计算机教师，自由编程界老兵一枚。

原文标题：​​Beyond Attention: How Advanced Positional Embedding Methods Improve upon the Original Approach in Transformer Architecture​​，作者：Elahe Aghapour & Salar Rahili