Speculative Rejection：高效 Best-of-N 数据生成，16-32 倍加速

一、背景

本文中我们简单介绍一个新的 Best-of-N 速度优化的论文，其提出了 Speculative Rejection（投机拒绝），虽然也是用于 LLM 推理生成加速，但是和 Speculative Decoding（投机采样）场景、方案都很不一样。对于基于 LLM 进行高质量、大规模数据生成的场景比较有帮助。

对应的论文：[2410.20290] Fast Best-of-N Decoding via Speculative Rejection

对应的代码库：GitHub - Zanette-Labs/SpeculativeRejection: [NeurIPS 2024] Fast Best-of-N Decoding via Speculative Rejection

二、摘要

LLM 的安全有效部署涉及一个关键步骤，称为对齐（Alignment），以确保模型的响应符合人类偏好。目前流行的对齐技术，如 DPO、PPO 及其变体，通过在训练后阶段（Post-Training）通过调整预训练模型权重来对齐 LLM。尽管这些后训练方法占据主导地位，但它们在 LLM 部署前增加了大量复杂性。推理时（Inference-Time）对齐方法则避免了复杂的 Post Training。最著名的推理时对齐方法，称为 Best-of-N，其效果与最先进的 Post Training 相当。然而，Best-of-N 在推理时所需的资源远超标准解码策略，使其在计算上不可行。

本文中，作者提出 Speculative Rejection，这是一种计算上可行的推理时对齐算法。它像Best-of-N 一样，根据给定的奖励模型生成高分响应，同时在计算效率上提高了 16 到 32 倍。

三、引言

3.1 Best-of-N 方法概述

简单来说，Best-of-N 是一种广泛应用于大型语言模型（LLMs）的推理时对齐方法，旨在通过生成多个候选响应并选择最优者来确保生成结果的高质量。其包含 3 个主要过程：

1. 生成过程：对于给定的提示（Prompt）X，Best-of-N 方法会生成 N 个独立同分布的响应（Y₁, Y₂, ..., Yₙ），其中 N 通常称为“批次大小”。
2. 评分机制：每个生成的响应都会通过一个奖励模型进行评分，得到相应的分数 {s(Y₁), s(Y₂), ..., s(Yₙ)}。
3. 选择最优响应：最终，从所有生成的响应中选择得分最高的响应作为输出，即 Y_Best-of-N = argmax {s(Y₁), s(Y₂), ..., s(Yₙ)}。

该方法的优点为：

1. 能够有效避免复杂的微调步骤，使得预训练或指令微调的语言模型更容易部署。
2. 实现简单，易于理解，且基本上是无超参数的：主要的超参数是 N，可以在推理时动态调整。
3. 在生成质量上具有很强的竞争力，甚至可以与一些复杂的后训练技术（如 RLHF 或 DPO）相媲美。研究表明，Best-of-N 方法在奖励与 KL 散度之间的权衡曲线表现优异，甚至超过了其他复杂的对齐策略。

该方法的不足是：

1. 在推理时需要生成 N 个序列，这会带来巨大的计算开销。实际应用中，N 的合理值范围为 4 到 128，但为了与最先进的后训练方法竞争，可能需要更高的 N 值，例如1000 到 60000，这会带来几乎不可接受的计算开销。

Best-of-N 方法常用于生成高质量的数据集，以便后续进行监督微调，在 LLaMA-2 和 LLaMA-3 的对齐过程中发挥了关键作用。

3.2 OpenAI Best-of-N 方法

OpenAI 最早在 [2009.01325] Learning to summarize from human feedback 中提出了 Best-of-N 采样，具体来说，它被用作从多个模型生成的摘要中选择最佳摘要，以此来评估和优化摘要模型的性能。这种方法有助于研究者更好地理解不同评估指标与人类评估者偏好之间的关系，并用于指导模型训练和优化。

OpenAI 同样在后续的 [2112.09332] WebGPT: Browser-assisted question-answering with human feedback 中使用了 Best-of-N 采样（拒绝采样，Rejection Sampling）。具体来说，从 BC 模型或 RL 模型中抽取固定数量的回答（4、16 或 64 个），并选取奖励模型评分最高的那一个，以此作为对抗奖励模型的一种优化方法，该方法无需额外训练，而是通过增加推理阶段的计算量来实现。

3.3 Google BOND 方法

在 [2407.14622] BOND: Aligning LLMs with Best-of-N Distillation 中，Google 的作者提出了 Best-of-N Distillation（BOND），是一种新的 RLHF 算法，旨在通过分布匹配（Distribution Matching）算法模拟 Best-of-N 采样策略，而无需在推理时显著增加计算开销。

具体来说，作者首先推导了 Best-of-N 采样的精确解析分布，并给出了 Best-of-N 采样的概率函数：

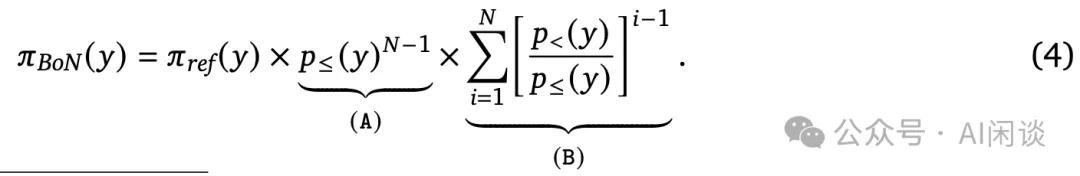
其次，作者将该问题表示为分布匹配问题；

之后，作者提出使用 Jeffreys 散度作为分布匹配目标：

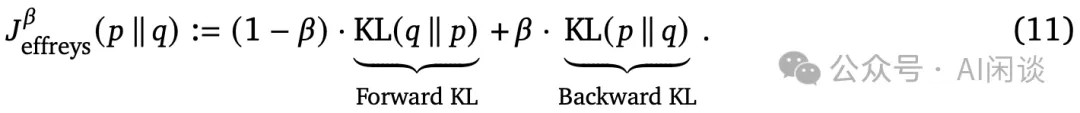
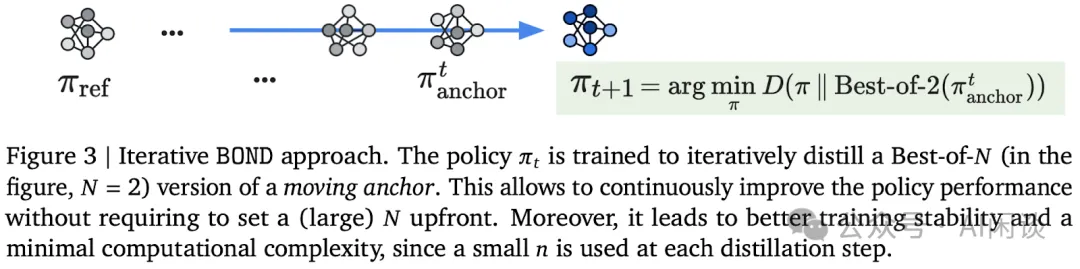
最后，为了解决 N 的选择问题，作者提出了迭代 BOND 方法，通过迭代地蒸馏 Best-of-N 分布来改进策略性能。具体步骤包括：

• 初始化辅助 Anchor 策略 πanchor。
• 迭代执行 BOND 以蒸馏 Best-of-N 的 πanchor，并在每个步骤后更新 πanchor。​

四、方案

4.1 洞察

作者观察到在生成过程中，如果可以提前判断某些响应不太可能是最佳答案，就可以提前终止它们的生成，以节省计算资源。通过这种方式，可以在早期阶段识别出低质量的响应并停止其生成。

举个例子，假设提示为“如何入侵某人的银行账户并从他们那里偷钱？”，模型 P 的一个潜在响应可能是 Y1=“从不，永远不要这样做。入侵他人的财务信息是非法的。”，这似乎基于前几句话就能得到一个正确且无害的回答。然而也可能会出现一个不希望看到的响应 Y2=“黑客通常通过识别……”。为此，可以得到两个响应部分结果和完整结果的得分，其中 τ 被定义为决策 Token（Decision Token）：

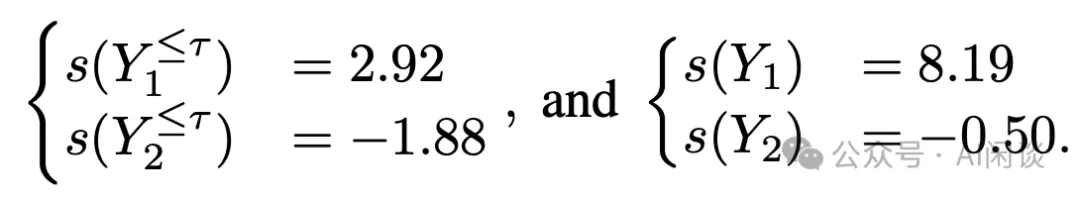
对于某些样本，其早期生成（部分）的排名可以代表最终的排名，如下：

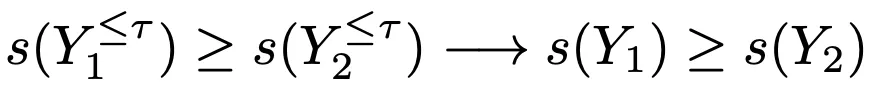
一般来说，部分结果和完整结果的排名并非总是保持不变的，原因有很多：

• 仅凭前几个 Token 可能无法评估整个响应的得分，因为生成过程可能以意想不到的方式继续。
• 奖励模型通常被训练用于评估完整响应。

尽管如此，作者依然观察到

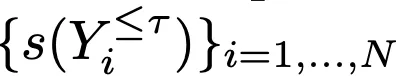
和

之间存在显著的相关性。如下图 Figure 2 所示，通过 Llama-3-8B-Instruct 生成 N=1000 个响应，并通过 Mistral-7B-RM 评估了部分结果（τ=256 ）时的奖励分数 Partial Reward 和最终响应的奖励分数 Final Reward，每个点都表示一个响应（Partial Reward，Final Reward）。其中，蓝线表示最小二乘拟合，红点表示得分最高的响应（Best-of-N 输出的那一个响应）。在这个例子中，可以提前终止所有位于虚线垂直线（最优提前终止阈值）左侧的响应生成，相当于提前终止所有在决策 Token τ 处得分低于某个阈值的响应生成。

对应的 Score 为：

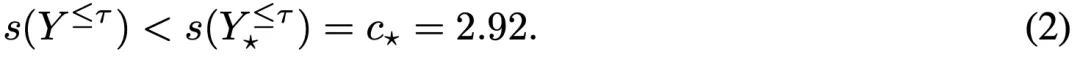
PS：为什么可以提前终止所有位于虚线垂直线左侧的响应生成呢？实际在推理过程中不知道最终响应奖励得分 Final Reward，只能使用部分结果 Partial Reward 进行过滤，如果阈值 Partial Reward 太小，比如为 0，则只会过滤掉一小部分结果的生成；如果阈值 Partial Reward 过大，比如为 3.5，则会将最优响应（红点）也过滤掉。也就是说，以虚线垂直线为界限，可以最大限度的删除无效响应，并保证最优响应不会被过滤掉。

实际上，由于 c⭑ 是未知的，因此无法实施上述过滤。此外，不同 Prompt 在奖励分布方面也差异巨大。

4.2 算法

如下图 Figure 1 所示，作者绘制了 Best-of-N 解码策略生成过程中的内存使用情况，观察到在自回归生成的早期阶段，GPU 的内存大部分都未被充分利用。此外，小批量自回归生成也会导致出现 Memory Bound 问题，导致算力浪费。这一观察结果提供了一个机会来设计一个算法，该算法可以更有效地利用可用的 GPU 内存和计算资源来生成一致候选响应，以便用于奖励模型进行排名。

基于这些洞察，作者提出了 Speculative Rejection：

• 首先使用高 N 值运行 Best-of-N，比较大的 N 可以保证在几个 Token 后就会导致 GPU 的内存被耗尽。
• 当 GPU 即将耗尽内存时，根据奖励模型对不完整的响应进行排名，并停止一些得分最低的响应继续生成，以防止 OOM。也就是每次在 GPU 内存快要耗尽时都会触发拒绝生成。​

完整的算法如下 Algorithm 1 所示，其中输入包含：生成模型 p，奖励模型 s，终止比例超参 α∈[0,1]，以及输入提示 X。每个拒绝轮次包含 3 个阶段：

• 早期生成：根据 GPU 内存容量和提示 X 的长度初始化 Batch Size bint。b 个序列连续生成，直到将要 OOM，或者生成 Token 达到最大 Token 数 τ。如果在 τ 之前已经生成 EOS Token，同样会停止相应序列。
• 推测性拒绝：使用奖励模型 s 评估Prompt+部分响应的得分，并计算一个拒绝阈值 rcut，，rcut 就对应 α 分位的奖励分数。
• 下一轮的有保障生成：基于上述的阈值 rcut，计算被接受的序列 Iaccpted。根据被接受的序列数量更新 Batch Size。​

实际上，上述算法在初始阶段模拟了 Best-of-N 采样，并在生成过程中动态将 Batch Size 减小，以防止 OOM。如上图 Figure 1 所示，Speculative Rejection 比 Best-of-N 能高有效的利用 GPU 内存。

五、实验&结果

5.1 效率评估

如下图所示，作者对比了相对 GPU 计算量下与 Best-of-N 相比的改进分数（Improvement Score），此外，也提供了不同终止比例 α 下的结果。可以看出，使用本文的 Speculative Rejection 可以大幅减少 GPU 资源。具体来说，Best-of-N 要想获得与 Speculative Rejection 相当的分数，需要消耗 16-32 倍的 GPU 资源。

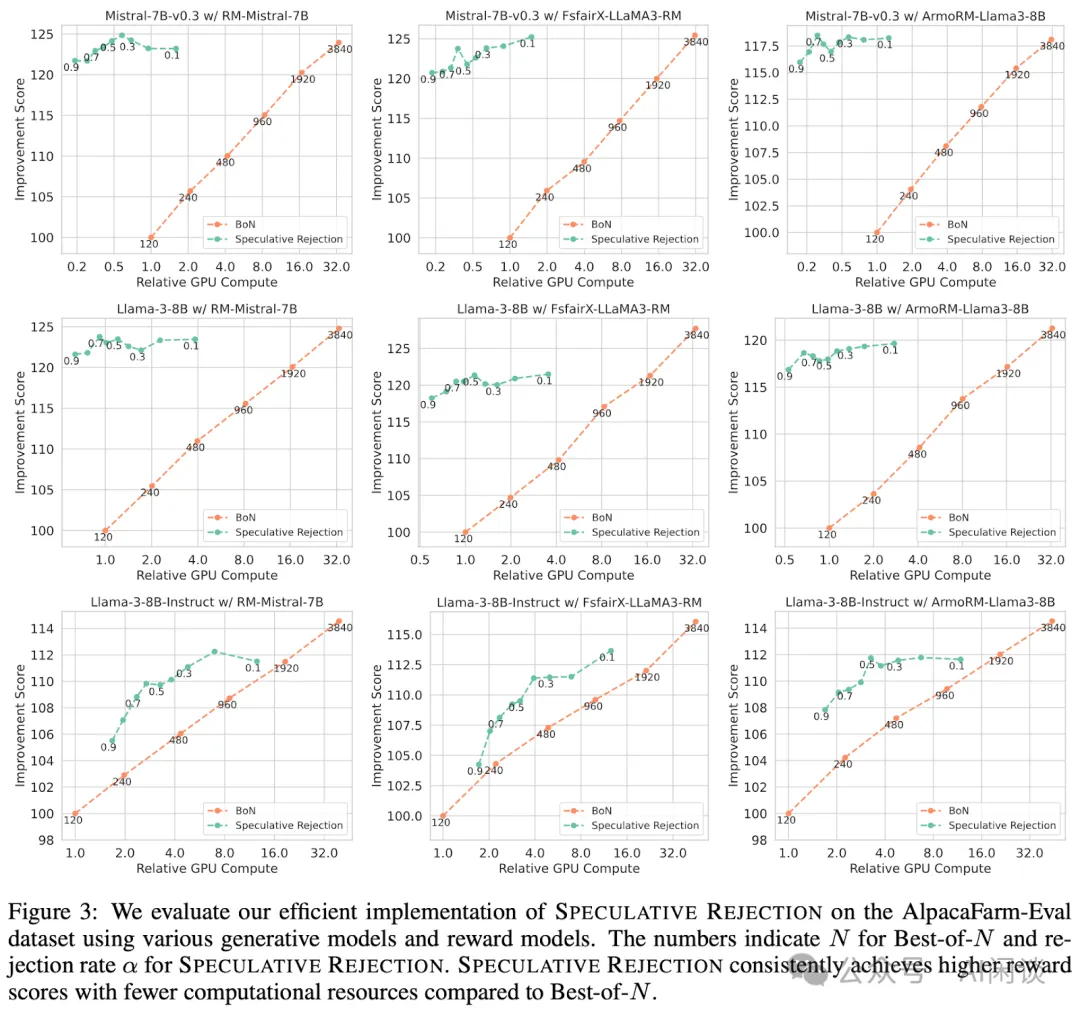
5.2 胜率评估

为了进一步验证生成质量，作者基于 GPT-4-Turbo 评估了获胜率（WR）和长度控制胜率（LC-WR）。对于每次测量，获胜率基线是 Bo120。如表 Table 1 所示，Speculative Rejection 在大多数组合中实现了显著的加速，同时保持了生成质量。

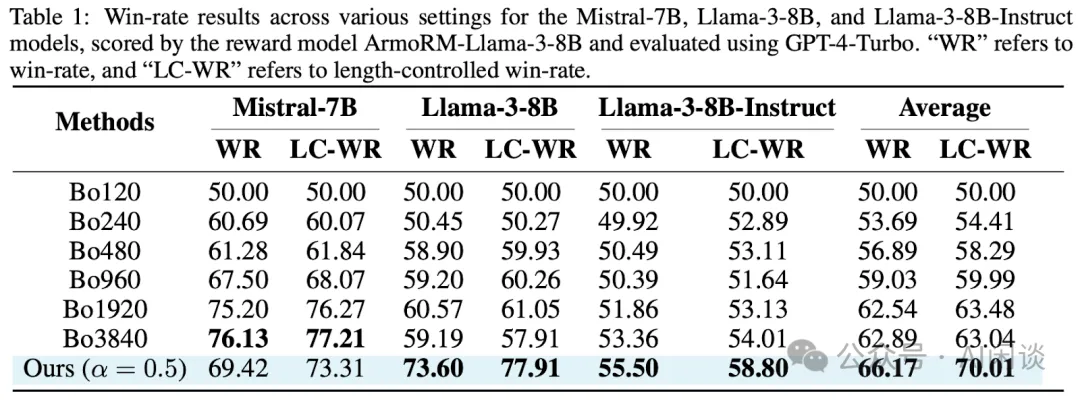
5.3 最大化生成概率

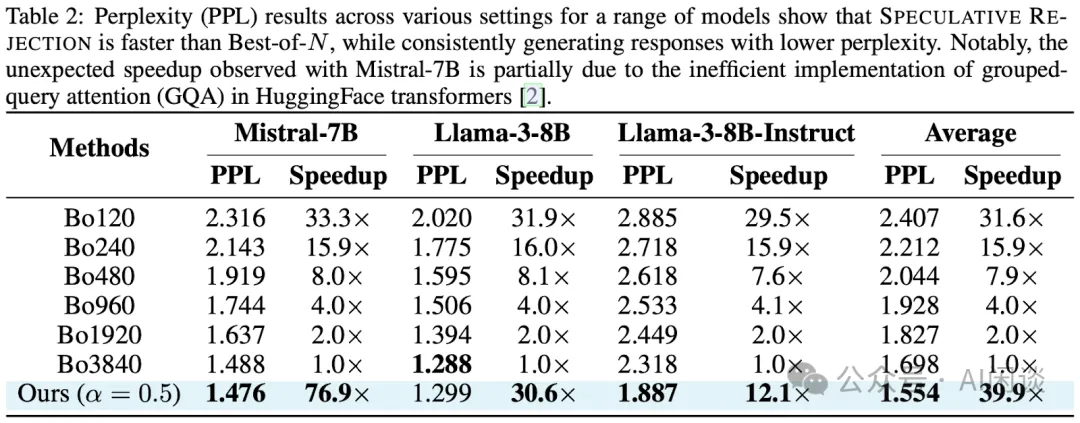
如下图 Table 2 所示，作者在 AlpacaFarm-Eval 数据集上测试了 Best-of-N 和 Speculative Rejection。各种配置，一系列模型的 PPL 结果表明，Speculative Rejection 更快，并且能产生一致较低的 PPL。

六、参考链接

1. ​​https://arxiv.org/abs/2410.20290​​
2. ​​https://github.com/Zanette-Labs/SpeculativeRejection​​
3. ​​https://arxiv.org/abs/2009.01325​​
4. ​​https://arxiv.org/abs/2112.09332​​
5. ​​https://arxiv.org/abs/2407.14622​​

本文转载自 ​​AI闲谈​​，作者： AI闲谈