Intel Smooth-SwiGLU:FP8 LLM 训练,34% 加速
一、背景
本文中我们继续介绍一个 Intel 最新的关于 FP8 训练相关的工作,其在一定程度上分析并解决了 FP8 训练中的不收敛问题,进一步推进了 FP8 训练落地(尤其是在 H100/H800 GPU 上)的可行性。
对应的论文:[2409.12517] Scaling FP8 training to trillion-token LLMs [1]
二、摘要
本文中,作者首次在 2T Token 的数据集上使用 FP8 精度训练了 LLM,比以前的限制增加了 20 倍。通过这些扩展训练实验,作者发现了 FP8 训练中的关键不确定性,这些不确定性在早期持续时间较短的训练中是无法观察到的。作者进一步追溯到 SwiGLU 激活函数的异常值放大问题。有趣的是,从分析和经验上表明,这些放大只发生在较长的训练中,并将其与 SwiGLU 的权重对齐过程联系起来。
为了解决这个新发现的问题,作者引入了 Smooth-SwiGLU,这是一种新颖的修改,可确保稳定的 FP8 训练而不改变函数的行为。作者还首次演示了两个 Adam 优化器参数(一阶矩和二阶矩)的 FP8 量化。
结合这些创新,作者在 256 个 Intel Gaudi2 加速器上使用 FP8 精度成功训练了一个 7B 参数量的模型,实现了与 BF16 基线相当的结果,同时提供了高达 34% 的吞吐提升。
三、引言
3.1 浮点数值表示
我们之前的文章中提到过,虽然都是 FP8 精度,但是不同硬件上存在不同的表示方式,主要包括 E5M2 和 E4M3,其中 E 表示指数位(决定了动态范围),M 表示尾数位(决定了表示精度)。此外,虽然都是 E5M2 或者 E4M3,不同的硬件可能采用不同的格式。比如 NVIDIA GPU 上的 E5M2 符合 IEEE 754 Style,而 E4M3 却不符合 IEEE 754 Style,可以称为 ARM-Intel-Nvidia Style。此外,AMD-Graphcore-Qualcomm 的表示也有所不同。如下图所示,IEEE 754 Style 的 E4M3 范围为 [-240, 240],而 ARM-Intel-Nvidia Style 的 E4M3 范围是 [-448, 448]:
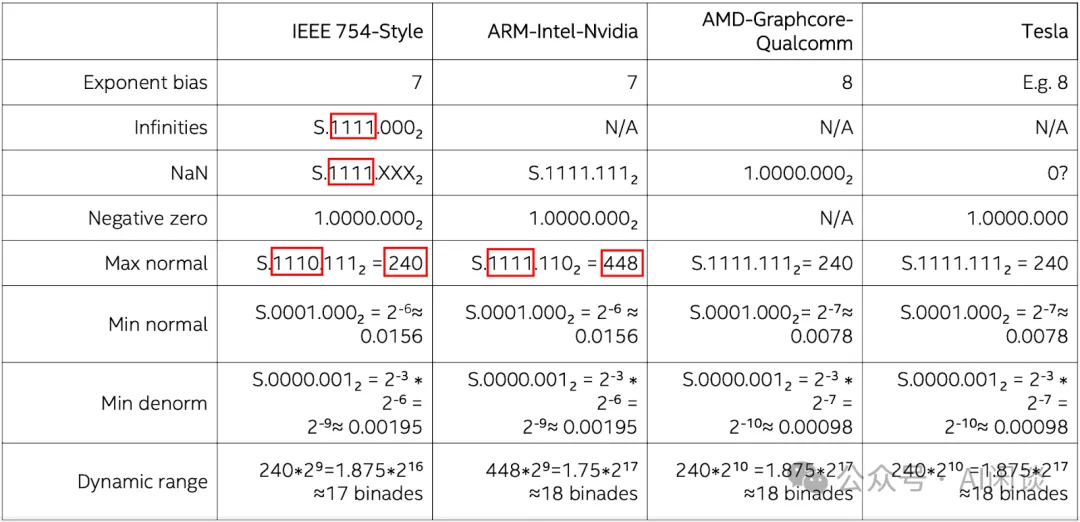
PS:由于 Intel 和 NVIDIA 采用一致的表示方式,这也就意味着 Intel 的结论能够很容易扩展到 NVIDIA 的 GPU。
3.2 SwiGLU
在 [2002.05202] GLU Variants Improve Transformer [2] 中作者提出了在 Transformer 模型中使用各种 GLU 变体激活,也提到其在许多下游理解任务上获得了更好的结果。然而,作者也提到并没有解释为什么这些修改会有效,将其归功于上帝的恩赐。在后续 Google 的 PaLM,Meta 的 LLaMA 系列等模型中广泛采用了 SwiGLU 激活。

如下图所示为 FFN 中应用 SwiGLU 的公式:
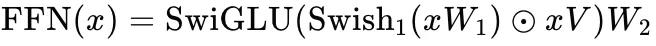
其中 Swish 为激活函数,可以表示为:
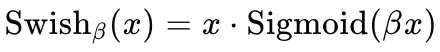
其 Pytorch 的实现也很简单,如下所示,这里用 silu 代替了 SwiGLU,对应 β 为 1:

因为这里有三个参数:w1,w2,w3,为了保证总参数量和正常 FFN 一致,所以 LLaMA 中这里的 Hidden Dim 不是 4d,而是 4d*2/3=8d/3。
3.3 GLU 类激活的离群点
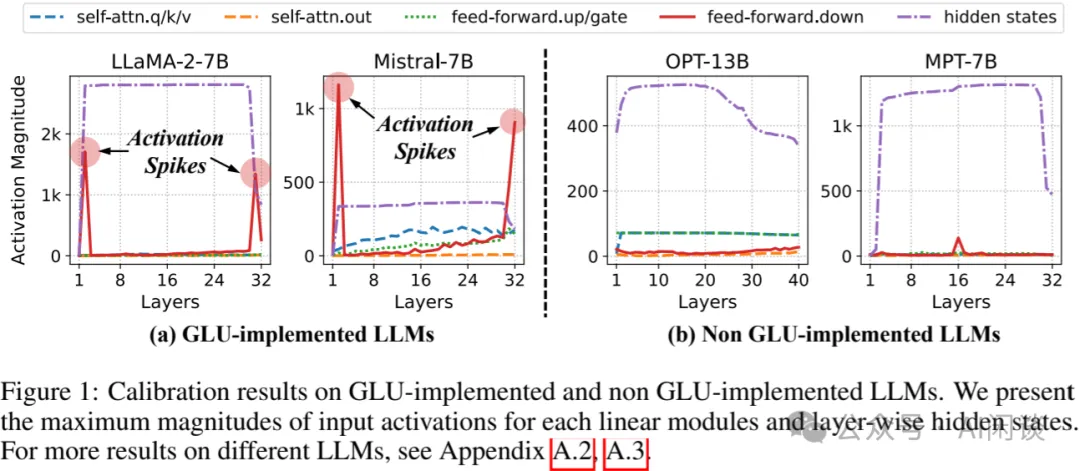
如下图 Figure 1 所示,在 [2405.14428] Mitigating Quantization Errors Due to Activation Spikes in GLU-Based LLMs [3] 中作者发现,各种 GLU 变体的激活函数容易在特定层(比如基于 SwiGLU 激活的 FFN 的最后一个 Liner 层的输入)出现激活的 Spike。此外,作者发现这些激活的 Spike 与中间层隐藏状态(Hidden Stage,每个 Transfomer Block 的输出)之间也存在高度相关性。并且 FFN 可能会通过残差连接中的加法运算放大 Hidden Stage。一旦 Hidden Stage 被放大,它就会在各层中持续存在,直到之后的层中再次遇到激活 Spike。
3.4 延迟缩放
在 FP8 的 Per Tensor Scaling 技术中,有两种常见的方式:Just-in-time Scaling 和 Delayed Scaling(可以参考 NVIDIA Transformer Engine 中的实现 Using FP8 with Transformer Engine [4])。
- Just-in-time Scaling(实时缩放):直接计算 Tensor 绝对值的最大值(amax),然后得到 Scaling 值,再对 Tensor 进行 Scaling。此种方法更加精确,但是,额外引入的开销会大幅降低 FP8 带来的收益。
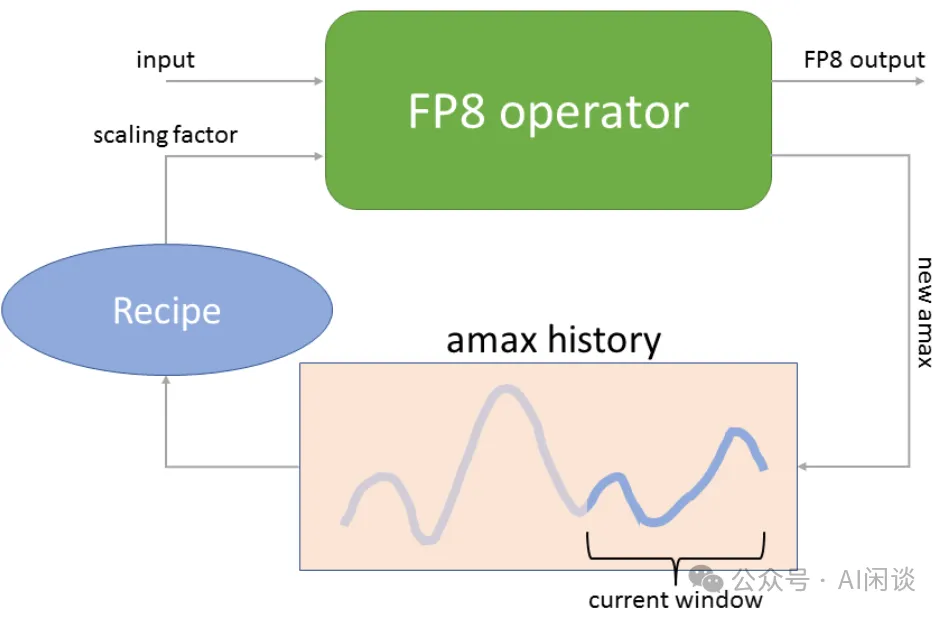
- Delayed Scaling(延迟缩放):核心思路是使用额外的 Tensor 来存储之前的 amax 历史,然后根据历史最大值估计当前的最大值。
如下图为 NVIDIA Transformer Engine 中的 Delayed Scaling 实现方案,amax history 最多可以存储 1024 个 history。在进行当前 Tensor 的 Scaling 操作时,使用当前 Tensor 之前的 amax history 来预测当前的 amax,然后再进行 Scaling 操作;Scaling 操作的同时会计算当前的 amax,并更新 amax history。
四、方案
4.1 洞察
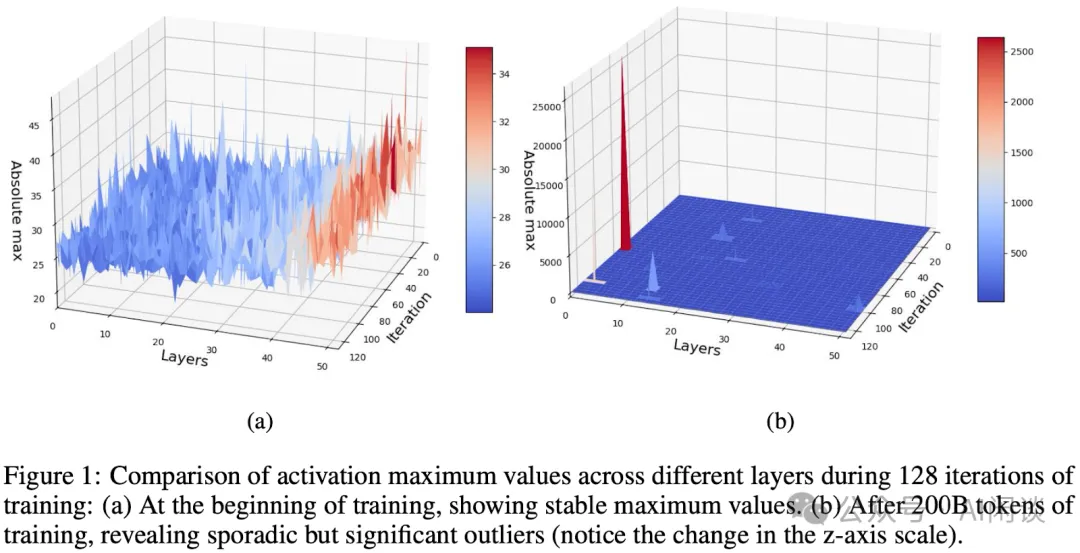
上面提到的 GLU 类激活引出的离群点(Outlier)问题会为 FP8 训练带来很多挑战。本文中,作者揭示,在大规模数据集上训练 LLM 的后期阶段,这些异常值变得尤为显著。
如下图 Figure 1 所示,(a)为训练的起始阶段,没有 Outlier;(b)为训练 200B Token 之后,出现偶发性的 Outlier。这些 Outlier 仅在训练中处理了很长一段时间才出现,此现象对维持训练中的数值稳定性带来极大挑战,进一步增加了 FP8 训练稳定性的难度,尤其是像 Megatron-LM 中广泛采用的延迟缩放方案中(如上述的介绍,这些方案假设了迭代期间的一致性)。
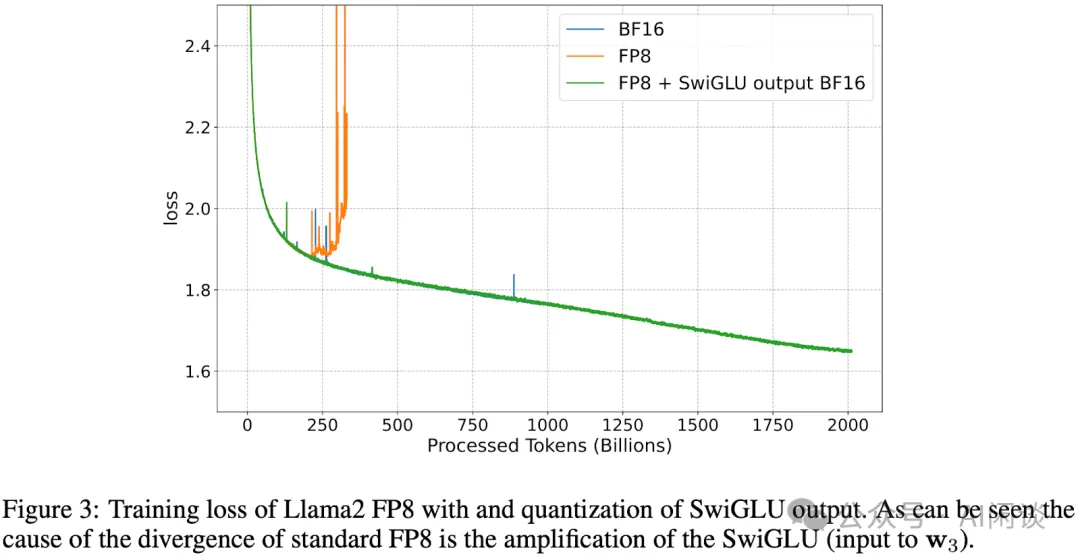
如前所述,SwiGLU 激活函数可能导致 FFN 组件的最后一个 Linear 层的输入出现 Outlier。在使用 FP8 训练,并采用延迟缩放技术时,SwiGLU 引发的 Outlier 会打破延迟缩放的统计一致性假设,导致训练过程的不稳定性。如下图 Figure 3 所示,作者展示了在 FFN 的最后一个 Linear (也就是 SwiGLU 的输出)禁用量化后的训练收敛性,LLaMA2 FP8 的训练能够成功地在大规模数据集上收敛,从而解决先前观察到的发散问题,这也验证了 SwiGLU 对 FP8 训练稳定性的影响。
4.2 SwiGLU 相关问题证明
如下图所示为 SwiGLU 的定义,其中,SwiGLU 由输入 x 与权重 w1、w2 进行乘积,分别得到 xTw1 和 xTw2。然后使用 Swish 激活函数对 xTw2 进行变换,将其与 xTw1 相乘。
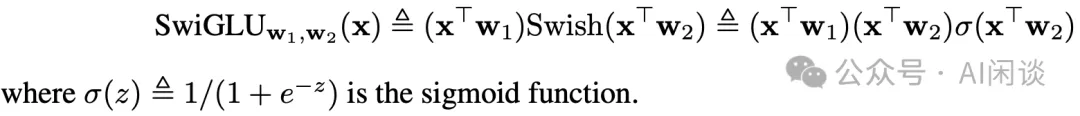
其他标准激活函数(如 ReLU、GeLU 和 Swish)在输入幅度较大时最多是线性的。这意味着当输入 u 逐渐趋于正无穷或负无穷时,这些激活函数的比值(即 ∣f(u)/u∣)会趋于小于等于 1 的某个值。然而,SwiGLU 是一个二次函数,可以达到更大的值,尤其在权重 w1、w2 相互“对齐”时(例如 w1=w2,并且 ||w1||=1)。
当 w1=w2 时,上式可以表示为:
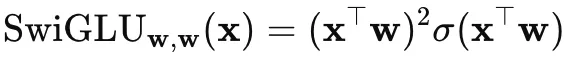
假设 xTw=c,则当 c 较大时,σ(c) 趋近于 1,此时下述结果约等于 c2,也就是上述所说的二次放大特性。
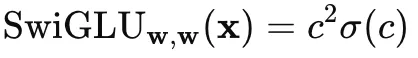
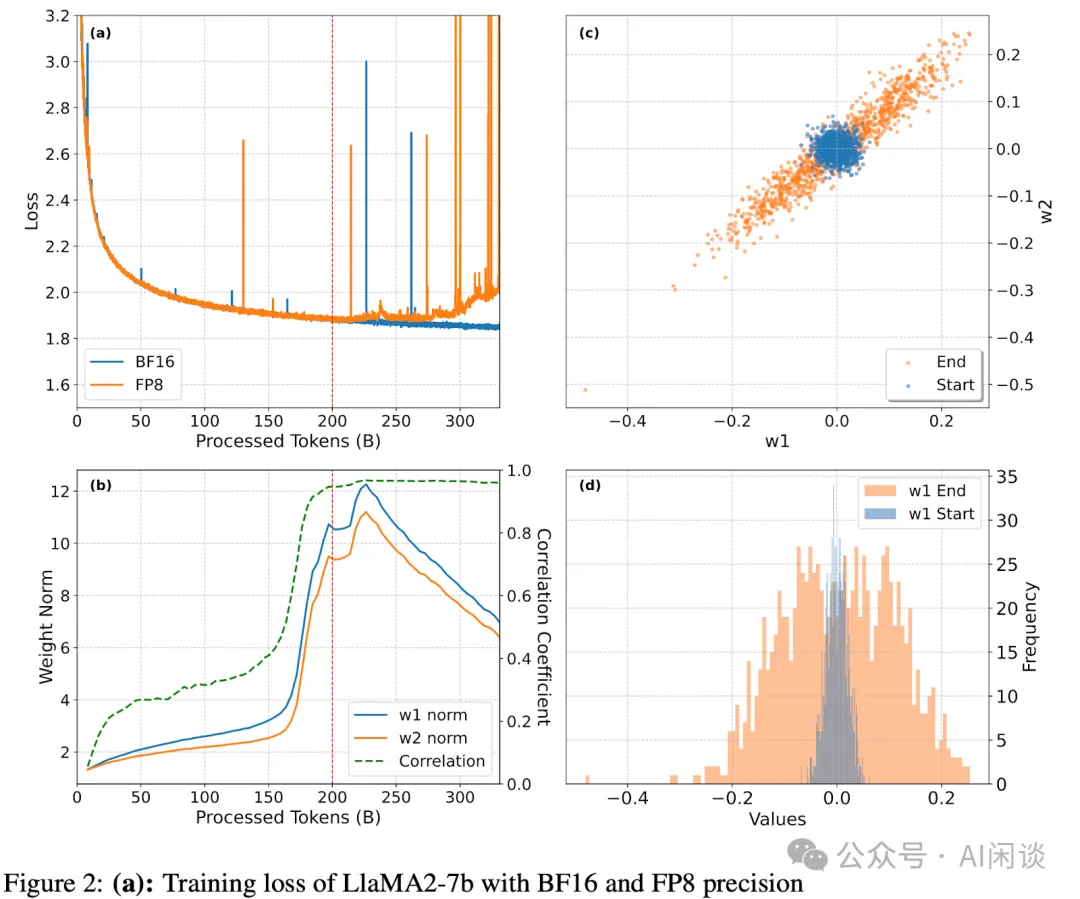
作者也进一步通过理论分析证明了上述 w1、w2 相互“对齐”现象,这里不再赘述,具体可以查看论文。当然,作者也进一步通过实验验证了相关问题。如下图 Figure 2 所示:
- (a):LLaMA2-7B 模型在 BF16 和 FP8 精度下的训练损失,其中 FP8 的训练在达到 200B Token 后开始出现明显的发散现象。
- (b):展示了某一个特定 Channel 在训练过程中 w1 和 w2 范数的动态变化及其相关性。
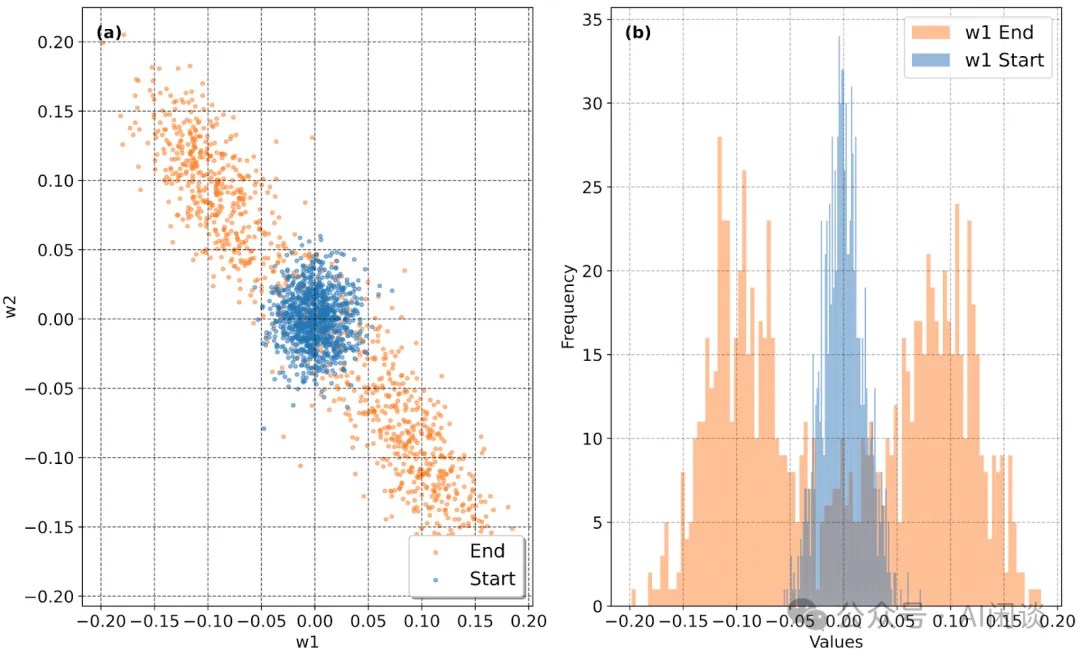
- (c):某一个 Outlier 通道在训练初期(8B Token)与后期(330B Token)w1 和 w2 元素散点图。可以看出,后期相关性显著提高,趋近于 w1=w2。
- 某一个 Outlier 通道在训练初期(8B Token)与后期(330B Token)w1 的直方图分布。
除了上图 (c) 那样的正相关性外,作者也观察到了明显的负相关性,也就是趋近于 w1=-w2,如下图所示:
4.3 Smooth-SwiGLU
为了在解决 Outlier 问题的同时保持完整的 FP8 加速,作者提出了 Smooth-SwiGLU 方法。如下图 Figure 4 所示,其展示了 Smooth-SwiGLU 的核心理念:对 SwiGLU 函数的线性分支施加一个缩放因子,并在最后一个 Linear 后将其重新缩放。此方法防止了输入到最后一个 Linear 的量化过程中出现 Outlier,同时保留了 SwiGLU 激活函数的整体功能,使能够在整个网络中充分利用 FP8 精度。
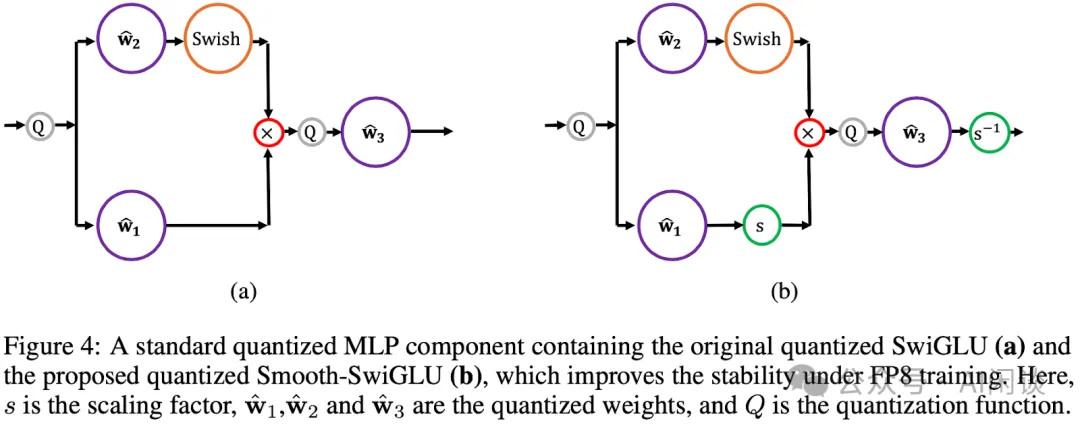
为降低计算开销,作者采用了一种高效的并行方法来计算缩放因子 si,也就是 Per Channel 量化:
1. 将 Tensor 分割成若干块,每块对应一个通道。
2. 对每个块(通道),并行计算其最大值。
3. 利用这些每个通道的最大值,确定各通道的独立缩放因子 si。
此方法实现了高效的逐通道缩放,因为每个通道的缩放因子是独立并行计算的。相较于 Linear 层中的矩阵乘法,这种方法的计算成本适中,尤其是在并行化处理下,即便在非优化实现中也是如此。在推理阶段,这些缩放因子可以合并到包含 SwiGLU 层及其后 Linear 的 FFN 的第一和第三Linear 的权重中。
五、实验&结果
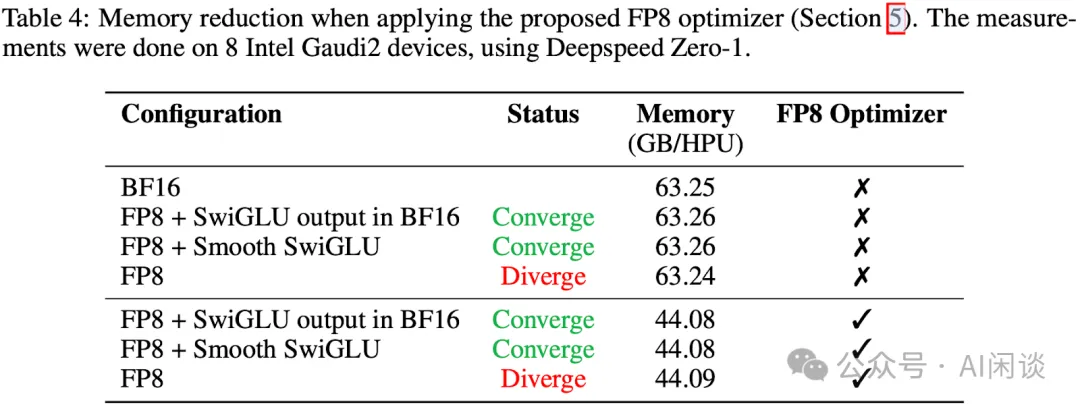
5.1 FP8 优化器
Adam 优化器及其变体在深度学习中得到广泛应用,Adam 优化器的一个关键特征是其存储两个矩,传统上采用高精度(FP32),这显著增加了内存开销,尤其对于大规模模型而言。尽管先前研究中已证明将其一阶矩降至 FP8 精度的可行性,但仍保留二阶矩为 FP16。本文中作者则更进一步,成功将二阶矩也量化至 FP8,显著提升了大型语言模型优化器的效率。
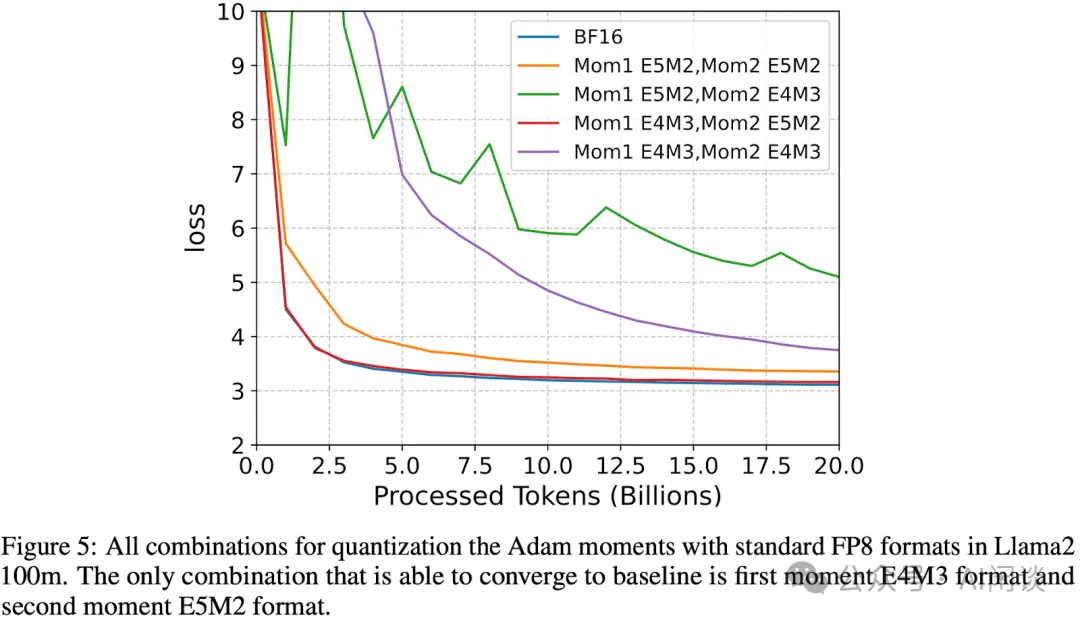
如下图 Figure 5 所示,作者探索发现一阶矩 Mom1 采用 E4M3,二阶矩 Mom2 采用 E5M2 可以很好的维持训练精度:
5.2 训练效果实验
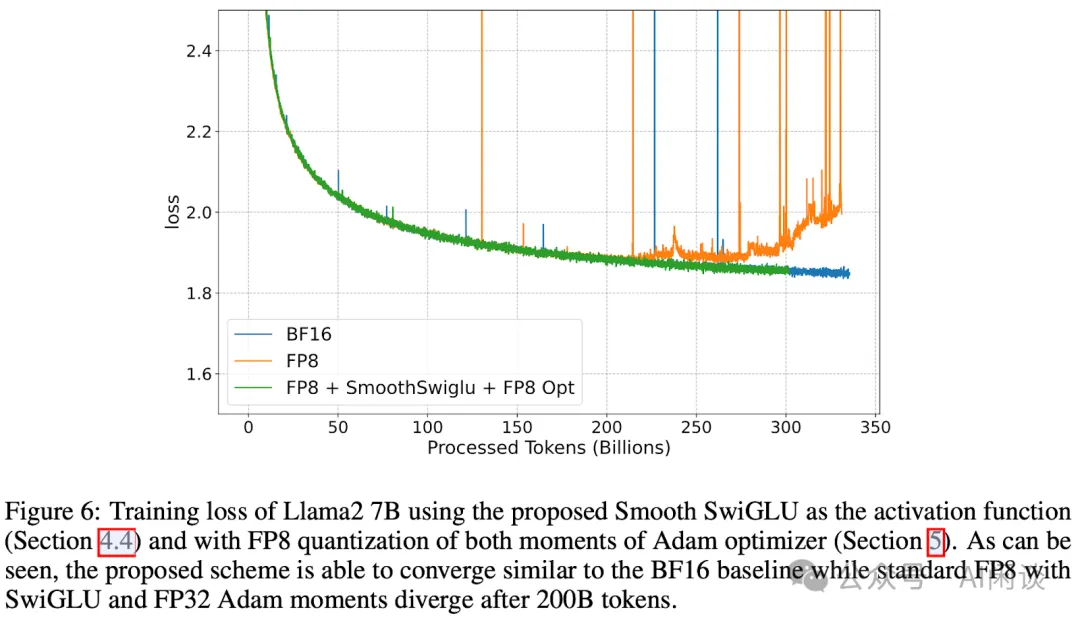
如下图 Figure 6 所示,作者在 256 个 Gaudi2 上训练 LLaMA2 7B 模型,共训练了 330B 左右 Token。本文的 Smooth-SwiGLU + FP8 优化器可以和 BF16 训练维持相当的 Loss,而传统的 FP8 训练在 200B Token 时开始发散。
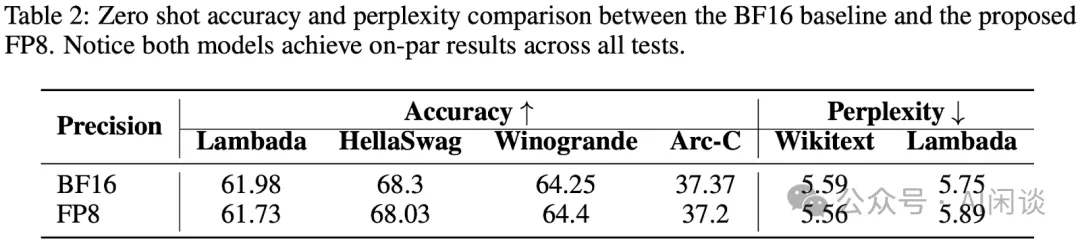
如下图 Table 2 所示,作者进一步对比了下游任务的 Zero Shot 精度以及困惑度,可以看出,本文 FP8 训练出的模型可以很好的保持精度:
5.3 训练速度
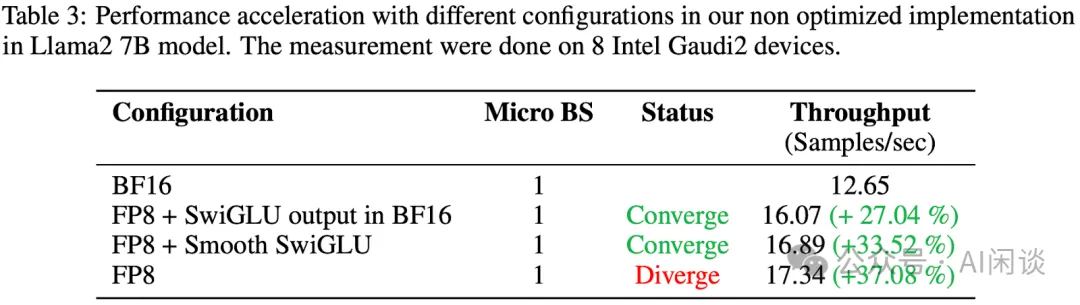
如下图 Table 3 所示,可以看出,本文方案在保持收敛性的同时获得了更高的加速比,相比 BF16 训练可以加速 33.52%(不及 FP8 主要是因为引入了一些额外的开销)。
虽然额外引入了一些计算开销,但显存并没有明显增加: