时序预测数据处理新方法汇总：多粒度和频域的可逆归一化

时间序列预测建模中，非平稳性或distribution shift一直是一个建模难点。非平稳性指的是时间序列的统计量，如均值、方差随时间发生变化，导致数据分布随着时间发生漂移，造成了模型训练和拟合的难度。

今天给大家介绍一下最近一段时间提出的2种解决时间序列非平稳性问题的方法。这两种方法分别从多粒度的角度和频域的角度进行可逆归一化，实现了不错的效果提升。

1.基础可逆归一化方法

可逆归一化最基础的方法来自REVERSIBLE INSTANCE NORMALIZATION FOR ACCURATE TIME-SERIES FORECASTING AGAINST DISTRIBUTION SHIFT（ICLR 2022），这篇文章的核心思路是在输入序列中将均值、方差等序列不稳定的信息去掉，再在输出阶段利用这些被去掉的不稳定但是序列个性化的信息对序列进行还原，模型重点处理去掉均值和方差后的平稳序列的预测任务。

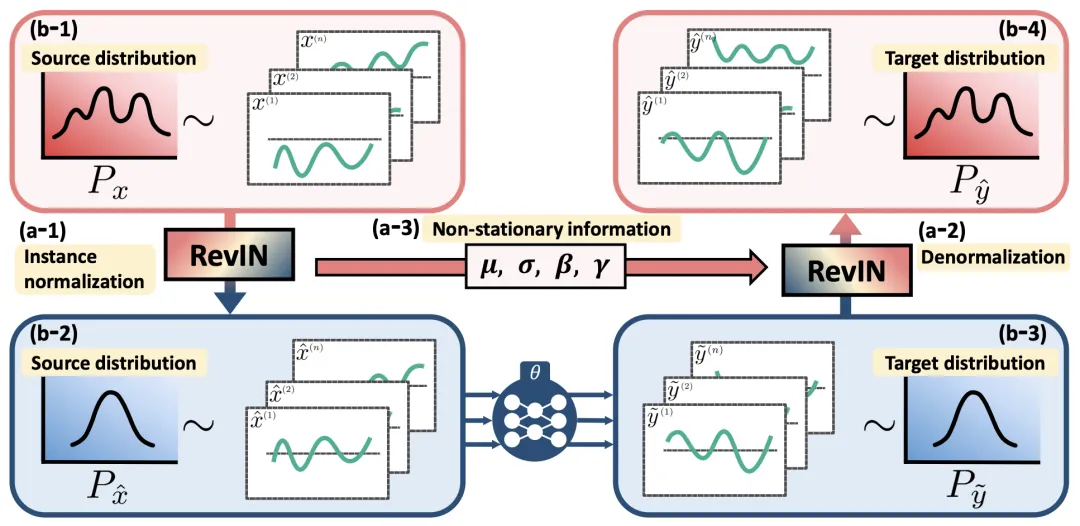
下面给大家进一步介绍最近两篇可逆归一化建模方法。

2.多粒度可逆归一化

论文标题：EVOLVING MULTI-SCALE NORMALIZATION FOR TIME SERIES FORECASTING UNDER DISTRIBUTION SHIFTS

下载地址：​​https://arxiv.org/pdf/2409.19718v1​​

上述基础的ReVIN只考虑了单一粒度的统计量信息，没有考虑多粒度信息的影响。时间序列中，不同的粒度的序列，对应的均值和方差都是存在较大差异的，只用单一粒度的统计量进行归一化，无法完美解决分布漂移问题。

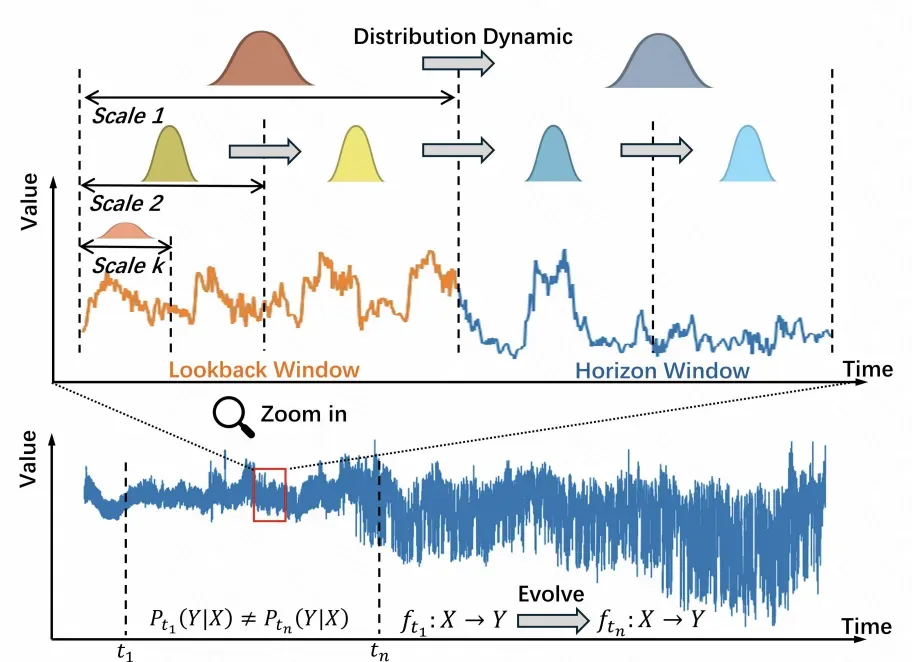
为了解决上述问题，本文提出了一种多粒度归一化方法。对于原始时间序列，先经过傅里叶变换后，找到topK个主成分，这些主成分表明序列的主要季节性信息。接下来，根据这些频率信息作为聚合粒度，生成K种不同粒度的时间序列聚合结果。针对每种粒度的时间序列，分别使用类似Dish-TS的建模方法，进行均值方差的归一化，并预测未来的均值方差，再将预测的均值方差作用到模型输出结果上。对于不同粒度的预测结果进行ensemble，使用频域中该粒度对应频域的振幅进行加权，得到最终的预测结果。

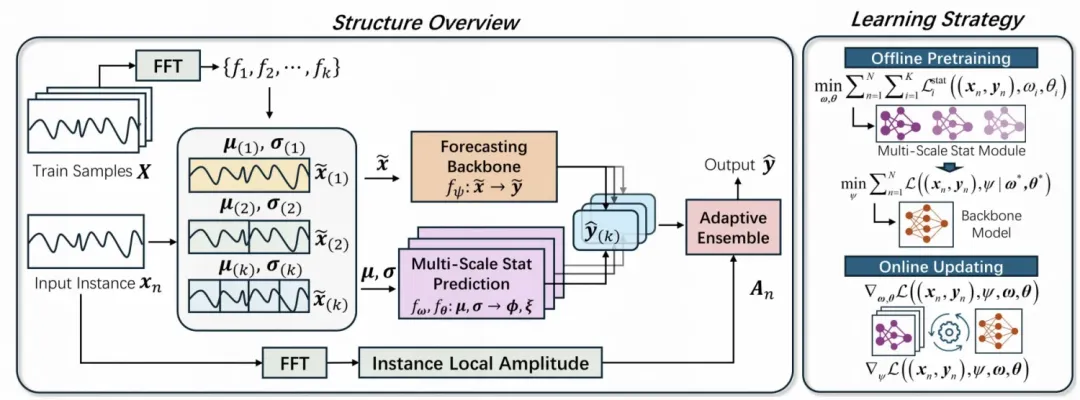
3.频域可逆归一化

论文标题：Frequency Adaptive Normalization For Non-stationary Time Series Forecasting

下载地址：​​https://arxiv.org/pdf/2409.20371v1​​

ReVIN这种在时域进行的可逆归一化方法，虽然能解决均值和方差的变化问题，但是无法解决周期性的变化问题。比如图中，模型的季节性随着时间发生变化，这个信息在ReVIN的方法中无法消除。

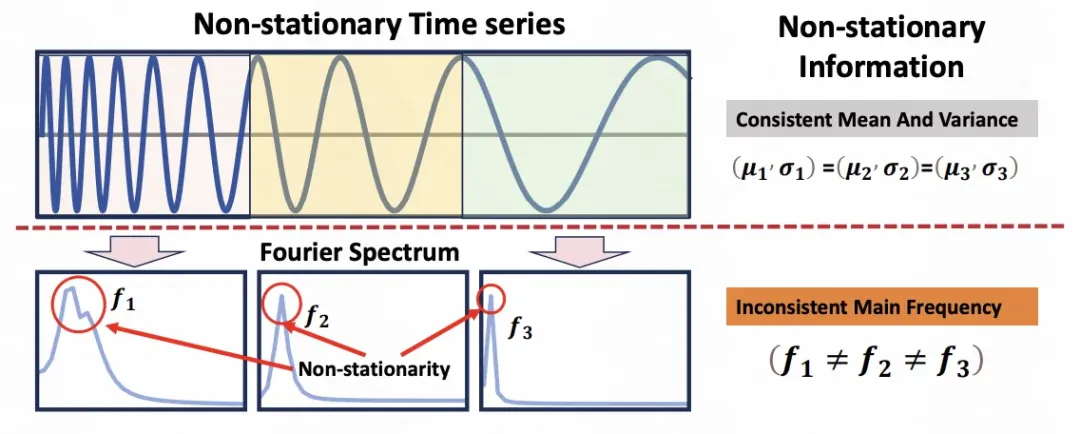
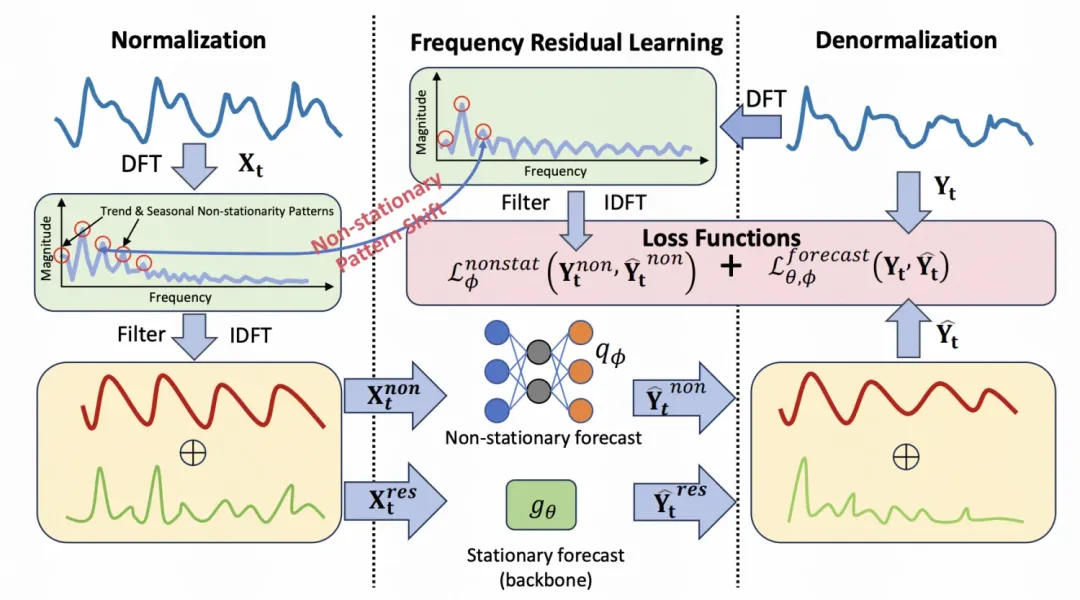
为了解决这个问题，这篇文章提出了一种在频域进行可逆归一化的建模方法。其整体建模思路和ReVIN类似，将原始序列通过傅里叶变换映射到频域，在频域中选择topK个主要频率成分，将这些主要频率成分从原始数据中剥离出来，模型只对剩余的平稳季节项的序列进行预测，预测结果再加上主要频率成分进行还原。

4.总结

分布漂移是时间序列预测的一个核心研究点，也是建模的难点。今天介绍的2篇新方法，从不同维度提出了新的时间序列可逆归一化建模方法，取得了一定的效果提升，可以在实际应用中进行尝试。

本文转载自​​圆圆的算法笔记​​，作者： Fareise ​​​​