无法解释LLM的智能涌现,可以从神经元的基本原理入手 原创
大模型如Llama 3.1 8B、70B、405B(即80亿、700亿、4050亿参数)中的这些几十亿、几百亿、几千亿的参数主要是指模型中所有可训练的权重和偏置的总和,这些参数分布在模型的各个层、节点和组件中,用于学习数据的复杂表示并生成预测结果。

“大力出奇迹”,即“Scalling Law”:在保持模型架构和训练策略不变的情况下,通过简单地增加模型的参数数量、训练数据量或计算资源,可以在一定程度上提升模型的性能。这种趋势在多个大型语言模型的实验中都得到了验证,表明在当前的技术水平下,参数规模的增长仍然是推动模型性能提升的重要因素。
能够大力出奇迹,可能来源于大模型是由无数简单的神经元构成,就像蜂群由无数工蜂组成。越是简单的个体,不断叠加个体的数量,一定会量变到质变,产生智能涌现。
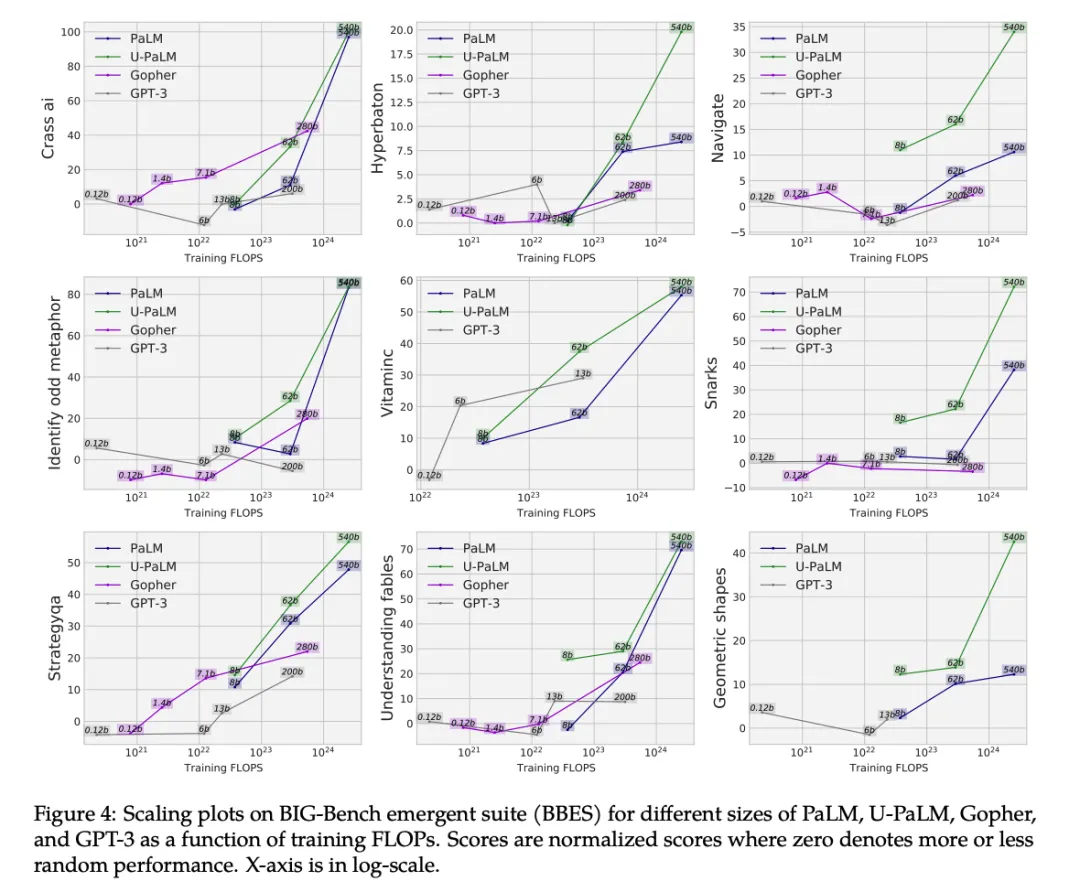
这一切的逻辑,背后的理论支撑是什么?机器学习(Machine Learning)时代已经出现了,从数学的角度那是更早就有了。即神经网络中单个神经元:y = σ(wx + b),线性回归再叠加一个激活函数。
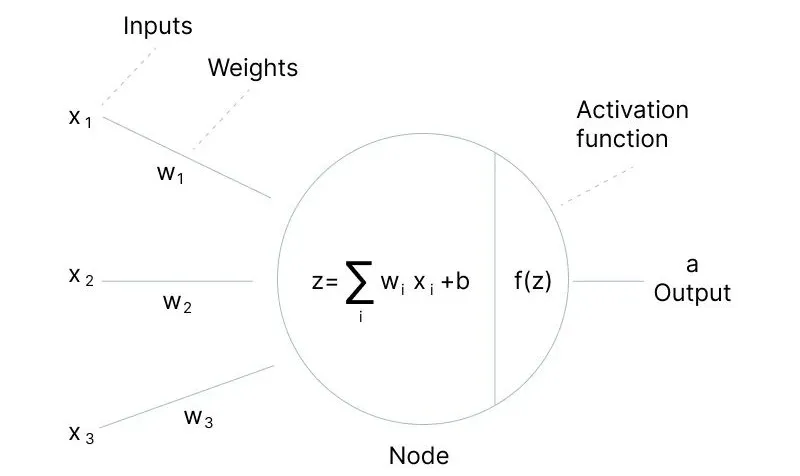
神经网络中单个神经元
大语言模型(LLM)动辄上千亿的参数如何“大力出奇迹”,如何遵守“Scalling Law”,如何产生“智能涌现(Emergent)”?这些目前都无法证明、不好理解,但是单个神经元的工作原理我们还是能搞清楚的。想搞懂大模型,那就先从了解权重w、偏置b以及激活函数开始吧。

神经网络的重要参数
权重w和偏置b:在神经网络中,模型参数包括每一层的权重(weight)和偏置项(bias)。这些参数在训练过程中通过反向传播算法进行调整,以最小化损失函数。神经网络模型参数的数量和复杂性随着网络层数和每层的神经元数量的增加而增加。
- 权重(w):用于描述不同神经元之间的连接强度。在神经网络的前向传播过程中,输入数据会与权重进行加权求和,从而影响神经元的输出。
- 偏置(b):用于调整神经元的输出。偏置的作用类似于线性方程中的截距项,它使得神经元的输出可以偏离原点。
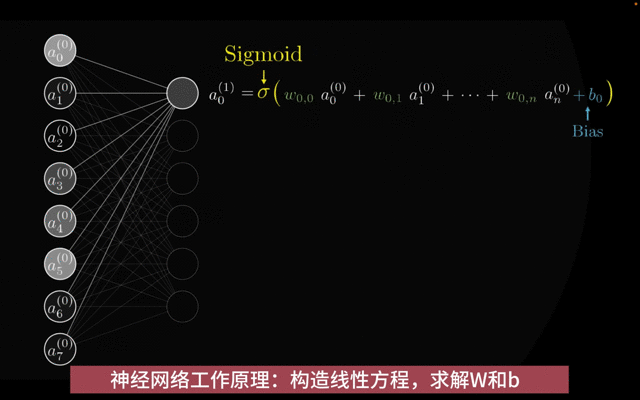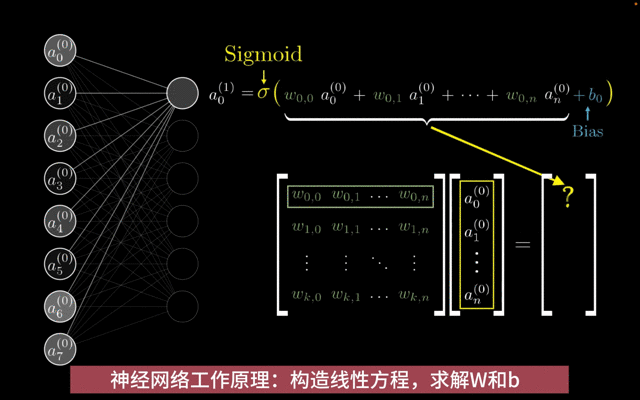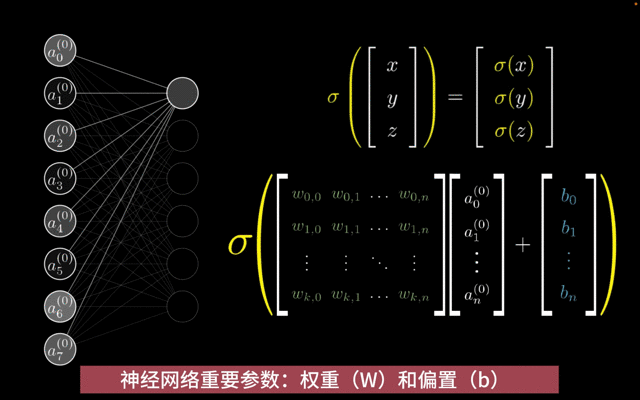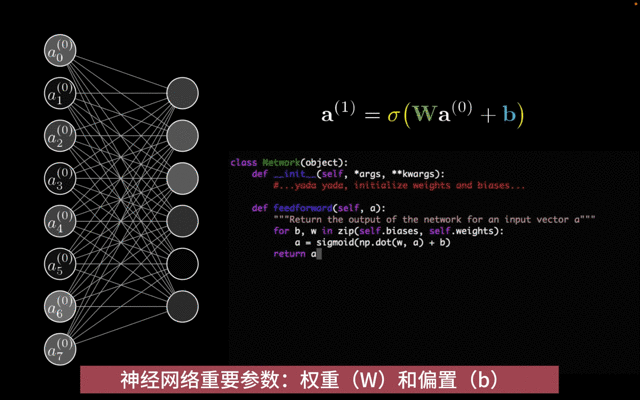
权重W和偏置b
激活函数:在神经网络中,输入通过加权求和(权重(w)和偏置(b)),然后被一个函数作用,这个函数就是激活函数。它决定了节点是否应该被激活(即,是否让信息通过该节点继续在网络中向后传播)。
神经网络中,如果只有线性变换,那么无论神经网络有多少层,输出都是输入的线性组合。引入非线性激活函数,使得神经网络逼近任何非线性函数。
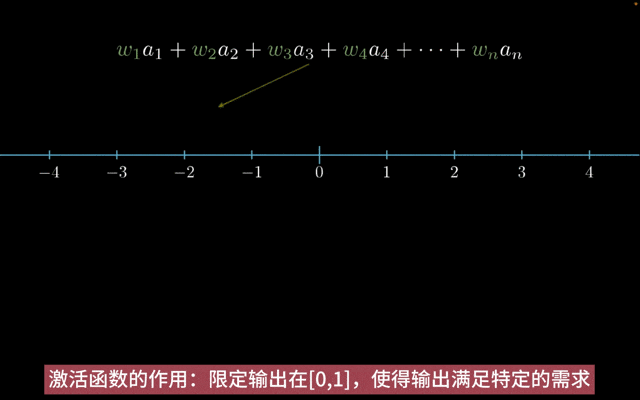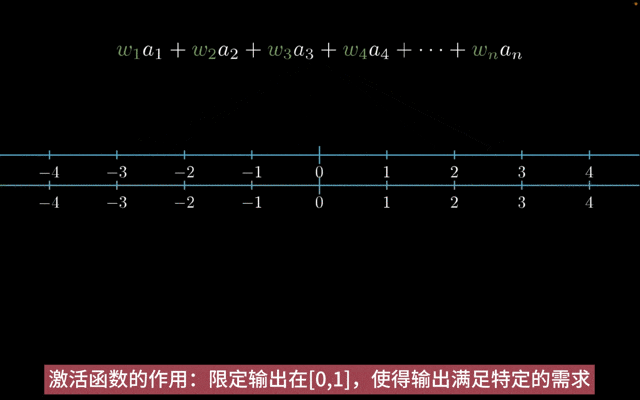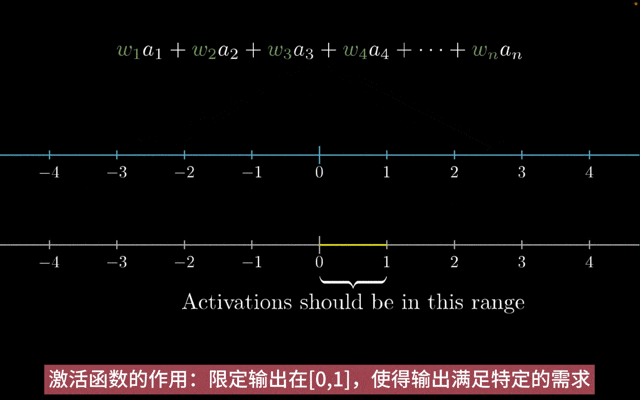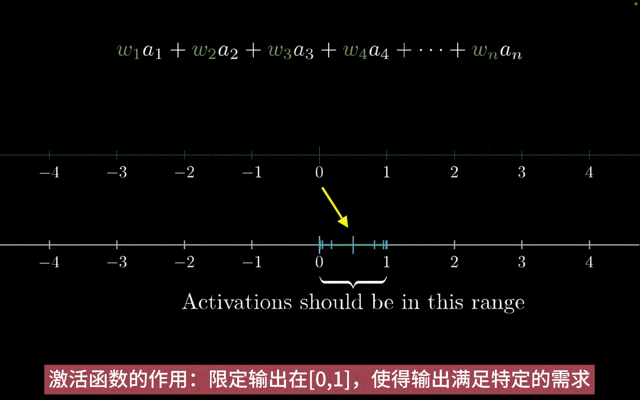
激活函数的作用
常见的激活函数包括:Sigmoid、Tanh、Softmax、ReLU、Leaky ReLU
- Sigmoid:将输入的连续实值压缩到0和1之间,特别大的负数映射为0,特别大的正数映射为1。但它存在梯度消失和输出不是以0为中心的问题。
- Tanh:将输入的连续实值压缩到-1和1之间,输出以0为中心。但它同样存在梯度消失的问题。
- Softmax:常用于多分类问题的输出层,将神经元的输出映射到概率分布上。
- ReLU (Rectified Linear Unit):当输入大于0时,输出等于输入;当输入小于等于0时,输出为0。ReLU解决了梯度消失的问题,但可能会导致神经元“死亡”的问题。
- Leaky ReLU:对ReLU进行了改进,当输入小于0时,给予一个很小的斜率,从而避免神经元“死亡”的问题。
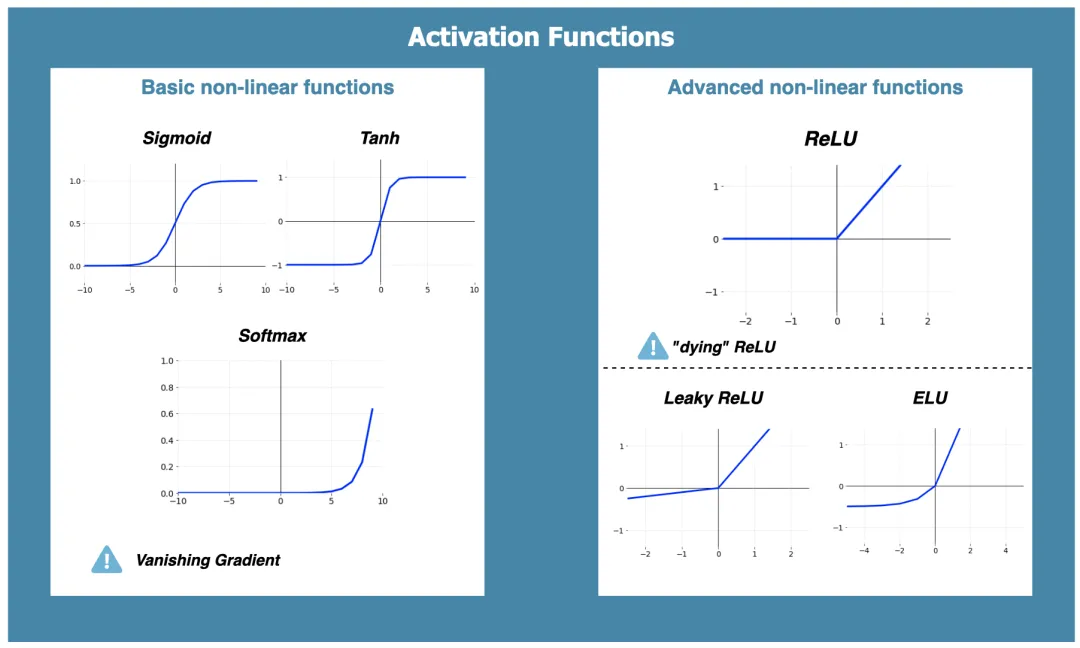
常见的激活函数
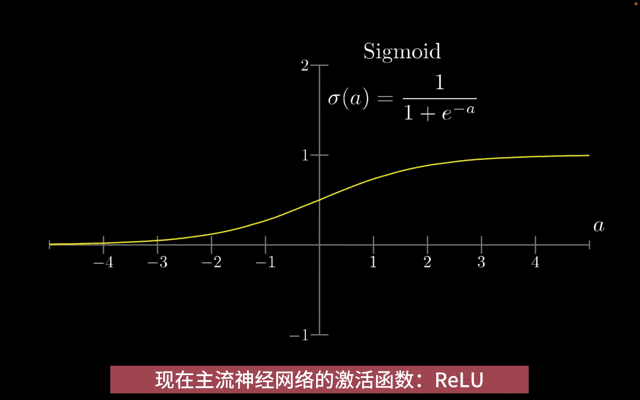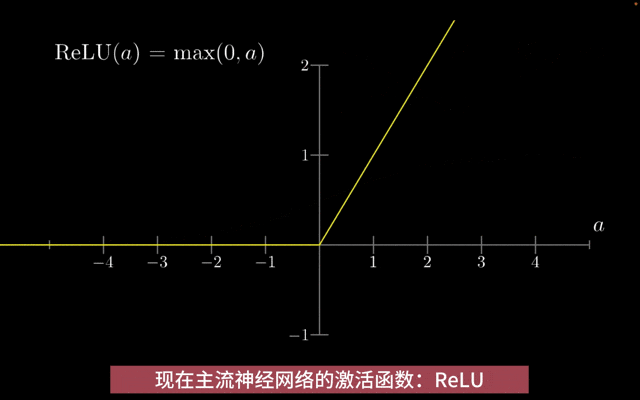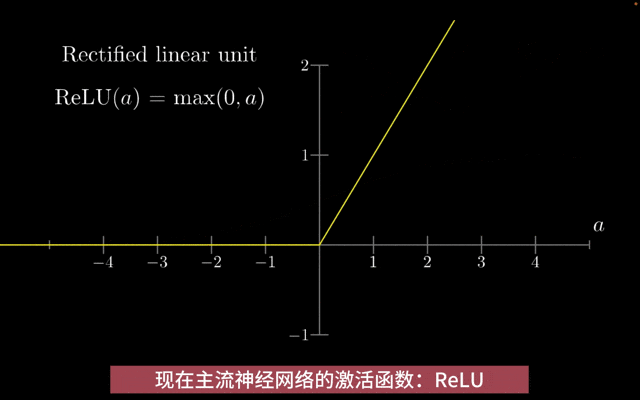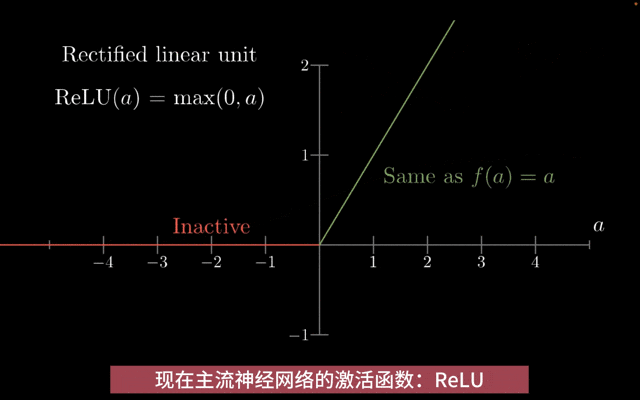
传统激活函数Sigmoid:Sigmoid 函数的输出始终在 0 和 1 之间,这使得它经常被用于二分类问题中,其中输出可以解释为属于某一类的概率。
与一些现代激活函数(如 ReLU)相比,Sigmoid 函数需要计算指数函数和除法操作,会增加计算成本,导致梯度消失/梯度爆炸问题。
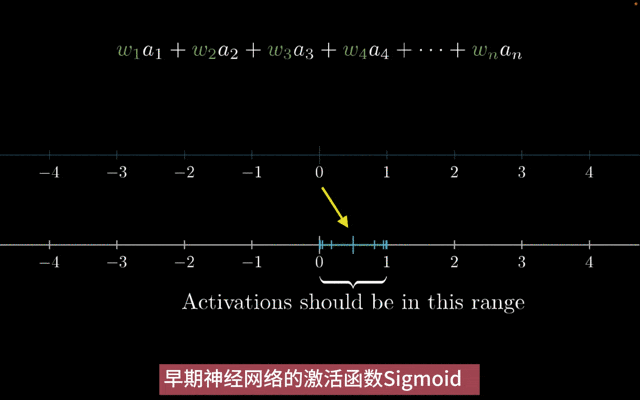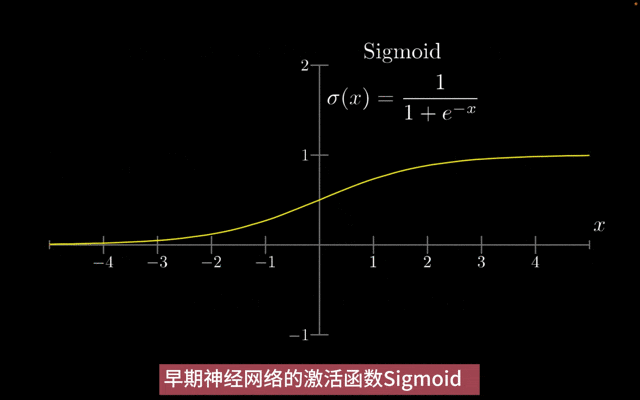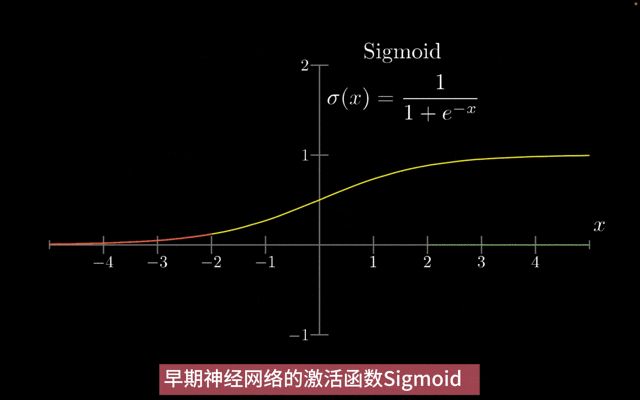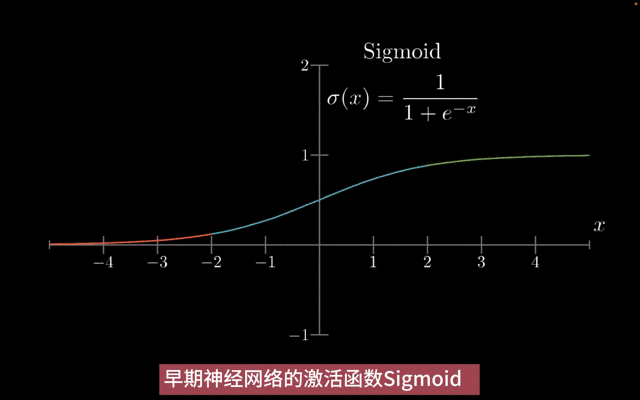
激活函数Sigmoid
主流激活函数ReLU:ReLU(Rectified Linear Unit)是当今深度学习领域中最主流的激活函数之一。
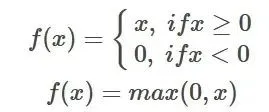
ReLU函数公式
ReLU与传统的Sigmoid和tanh激活函数相比,ReLU函数在输入为正数时导数为1,在输入为负数时导数为0,这有效地避免了梯度消失/梯度爆炸问题。由于ReLU函数的非线性特性和计算简单性,它可以帮助神经网络更快地收敛到最优解。
激活函数ReLU
参考资料
本文转载自公众号架构师带你玩转AI 作者:AllenTang
原文链接:https://mp.weixin.qq.com/s/e85gJmNewSD0AeSqUKgo7A
















