增加大模型推理能力的几个提示方法 原创

01.Complexity-based prompting for multi-step reasoning（ICLR2023)

基于复杂度的提示方法用于多步推理

摘要：我们研究了如何提示大规模语言模型进行多步推理。已有研究表明，当使用链式思考（CoT）提示，即用一系列短句描述从问题到答案的中间推理步骤时，大型语言模型能够为新的输入生成新的推理链并预测答案。本研究的核心问题是：哪些推理示例能成为最有效的提示？为此，我们提出了基于复杂度的提示方法，一种用于多步推理的简单且有效的示例选择方案。我们证明了具有较高推理复杂度的提示（即包含更多推理步骤的链）在多步推理任务上能显著优于强基线模型。此外，我们将基于复杂度的准则从提示（选择输入）扩展到解码（选择输出），在解码时，我们从模型中采样多个推理链，并选择复杂推理链中的大多数答案。通过这种方法，我们显著提高了GPT-3和Codex在多步推理任务中的准确性，并在三个数学基准（GSM8K、MultiArith和MathQA）和两个BigBenchHard任务（Date Understanding和Penguins）上实现了新的最先进表现，平均提升5.3个百分点，最高提升18个百分点。与现有的手动调优或基于检索的示例选择方案相比，基于推理复杂度的选择直观、易于实施，并且对标注的依赖较小。进一步的实验结果表明，复杂提示在格式扰动和分布偏移的情况下表现出鲁棒性。

图1 为链式推理提示（Chain of Thoughts Prompting，简称CoT）的工作流程，其中推理步骤用蓝色标注。整个流程包括：

- A部分：链式推理提示的工作流程。输入是一个问题，提示模型生成中间推理步骤（例如：通过几个步骤计算出问题的最终答案），然后基于这些步骤得出答案。该方法使用了一组链式推理案例，测试问题将从这些案例开始生成推理。

- B部分：显示了一个复杂的推理链的例子，包含9个推理步骤。相比之下，更简单的推理链可能只包含2步或3步。

- C部分：基于复杂性的一致性。该方法从模型中提取了多个推理链，然后通过对比复杂链的答案，选择较复杂链的多数投票答案作为最终结果。

整个流程的核心在于通过训练模型生成一系列推理步骤，并在答案中选择那些更复杂、更合理的推理链，以此提高准确率。

（注释：

A部分：链式推理提示的工作流程

1. 问题的输入：

比如，第一个例子的问题是：“Asia在促销中以140美元的价格购买了一件本来标价350美元的舞会礼服。她打折了多少？”

2. 推理步骤：

- 第一步：Asia省下了350美元 - 140美元 = 210美元。

- 第二步：她省下的210美元相当于原价的多少比例？答案是：210 ÷ 350 = 0.60 = 60%。

3. 生成答案：

最后模型给出的答案是60，即Asia在这次购买中享受了60%的折扣。

B部分：复杂的推理链

接着展示了一个复杂问题的解决方案：

问题：Angelo和Melanie想规划学习时间。他们每小时休息10分钟，计划在一周内完成学习。他们需要计划多少天来完成学习？

推理步骤：

1. 他们需要为两章内容各花3小时。

2. 为每个工作表花1.5小时。

3. 计划每天学习4小时，因此需要学习12小时，总共需要3天（12小时 ÷ 4小时/天）。

4. 他们不想每天学习超过4小时，计划学习15小时 ÷ 4小时 ≈ 3.75天。

5. 他们决定计划4天的学习，以确保时间充裕。

答案：最终答案是4天。

这部分演示了一个包含9个推理步骤的复杂推理链（相比之下，简单问题的推理链可能只需2到3步）。

C部分：基于复杂性的投票机制

在此部分展示了如何通过对复杂推理链的投票来获取一致答案：

1. 从模型中生成多个推理链：模型生成了五个推理链（A、B、C、D、E），这些推理链的复杂性不同，步骤数量从2步到6步不等。

2. 复杂链的一致性投票：每个推理链生成的答案有100或200。在本例中，通过复杂链投票，最终多数投票得出的答案是200。

这意味着在多个推理链中，复杂链往往能提供更准确的答案。模型倾向于通过分析更长、更复杂的推理过程来找到多数意见并将其作为最终答案。）

1、COMPLEXITY-BASED PROMPTING方法

1. 选择复杂示例作为提示（Selecting Complex Samples as Prompts）

这部分提出了一种新的示例选择策略，即优先选择复杂的推理链作为提示。作者假设，如果语言模型使用复杂的推理示例作为上下文学习，那么其推理性能会有所提升。复杂示例是指推理步骤较多的示例，这种多步推理能够包含更多的信息，因此有助于模型在推理过程中解决更复杂的问题。

具体而言，推理复杂性的衡量标准是推理步骤的数量，这一标准之前的研究中也有采用。作者进一步分析了其他可能的复杂性指标，如问题长度和公式长度，并发现这些复杂性指标在不同任务中表现出一致的效果，进一步验证了选择复杂推理链的有效性。

为了进一步减少标注成本，研究者还提出可以通过问题长度来识别复杂示例，然后仅为这些复杂问题手动标注推理链，减少了标注整个数据集的需求。

2. 复杂性一致性（Complexity-Based Consistency）

除了在输入空间（即提示）选择复杂示例外，作者还提出在输出空间上使用复杂性一致性的方法。通常情况下，推理模型在生成多个推理链时，可能会产生不同的答案。传统的多数投票方法是通过生成的所有推理链来选出答案。

然而，复杂性一致性方法通过对模型生成的多个推理链中的复杂推理链进行投票，而不是简单投票所有推理链。这意味着，在推理生成过程中，优先选择那些推理步骤较多的推理链来进行投票，进一步提高推理的准确性。

研究结果表明，与原始的一致性方法相比，复杂性一致性能更好地提高模型的推理能力。在实验中，投票复杂推理链的表现明显优于投票所有推理链，甚至远优于投票简单推理链的情况。

3. 实验验证（Empirical Validation）

在实验验证中，复杂性驱动提示方法在多个数据集上显著提高了表现，尤其是在数学推理任务（如GSM8K、MultiArith和MathQA）以及常识推理任务（如StrategyQA和Date Understanding）上。无论是采用复杂提示还是复杂一致性投票，该方法在大多数情况下均优于传统的提示策略，验证了推理复杂性在提高语言模型推理能力中的关键作用。

2、例子

假设有一个数学问题：

问题：

"Olivia有23美元。她购买了五个每个3美元的贝果。她还剩下多少钱？"

传统的语言模型可能会直接尝试给出答案，而不会详细解释推理过程。而在Chain of Thoughts（CoT）提示中，模型会先生成一系列中间推理步骤，如下所示：

简单提示（简单推理链）：

1. Olivia有23美元。

2. 她购买了5个贝果，每个3美元，所以她一共花费了5 3 = 15美元。

3. 她还剩下23 - 15 = 8美元。

答案：8美元。

这个简单的推理链只包含了3个步骤。在这种情况下，虽然能得出正确答案，但模型的推理能力没有被充分发挥。

而使用COMPLEXITY-BASED PROMPTING，我们会选择更复杂的示例来提示模型，可能包含更多的推理步骤，例如涉及其他类似问题的示例。

复杂提示（复杂推理链）：

1. Olivia有23美元。

2. 她打算购买5个贝果。

3. 每个贝果的价格是3美元。

4. 她购买的贝果数量是5个，因此总共花费是5 3 = 15美元。

5. 我们现在知道她花费了15美元。

6. Olivia的初始金额是23美元。

7. 23美元减去她的支出15美元，还剩23 - 15 = 8美元。

答案：8美元。

复杂性一致性：

在解答其他类似问题时，模型可能生成多个推理链。例如，模型可能产生以下不同长度的推理链：

- 推理链A：4个步骤，答案=8美元。

- 推理链B：5个步骤，答案=8美元。

- 推理链C：6个步骤，答案=8美元。

- 推理链D：7个步骤，答案=8美元。

- 推理链E：2个步骤，答案=错误。

使用复杂性一致性时，我们将优先选择那些推理步骤较多的推理链（如B、C、D），通过它们的多数答案进行投票，最终得出更准确的结果，而不是简单依赖所有推理链的投票结果。

Fu Y, Peng H, Sabharwal A, et al. Complexity-based prompting for multi-step reasoning[C]//The Eleventh International Conference on Learning Representations. 2022.

♠University of Edinburgh ♣Allen Institute for AI

--------------------------

02.Improving factuality and reasoning in language models through multiagent debate（PMLR 2024）

通过多代理辩论提升语言模型的事实性和推理能力

摘要：近年来，大型语言模型（LLMs）在语言生成、理解和少样本学习方面展现了显著的能力。大量研究致力于通过提示技术提升其性能，包括验证、自洽性或中间草稿。本文提出了一种互补的方法，通过多个语言模型实例提出各自的响应，并在多轮辩论中对各自的推理过程进行讨论，最终得出一个共同的答案。我们的研究表明，这种方法在多个任务中显著提升了数学和战略推理能力。我们还证明了该方法可以提高生成内容的事实准确性，减少现有模型常见的错误答案和幻觉现象。此方法可以直接应用于现有的黑盒模型，且在我们调查的所有任务中均使用相同的流程和提示。总体而言，我们的研究结果表明，这种“心灵社会”的方法有望显著提升大型语言模型的能力，并为语言生成和理解领域带来进一步的突破。

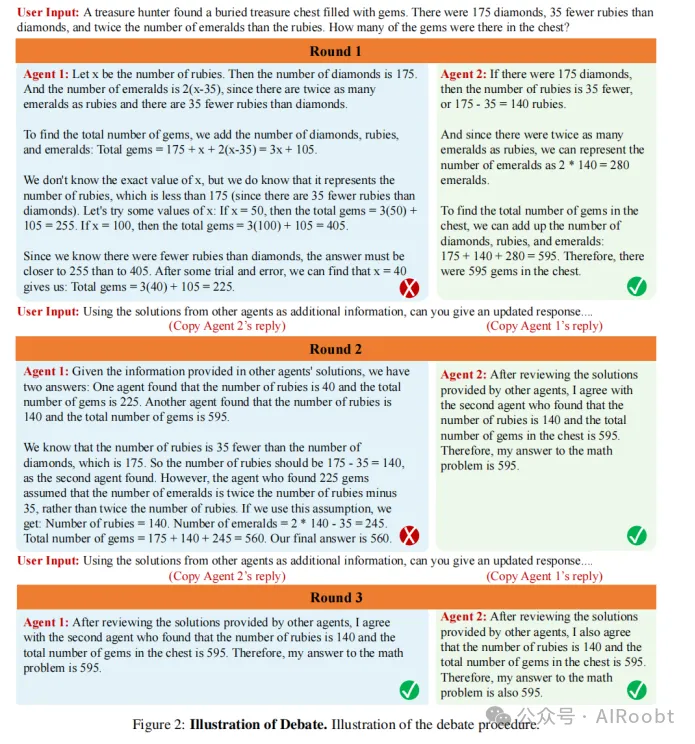
图2：辩论示意图。辩论过程的示意图。

（图片内容：

场景：一个寻宝者发现了一箱装满宝石的宝箱。箱子里有175颗钻石，红宝石比钻石少35颗，并且翡翠的数量是红宝石的两倍。宝箱里共有多少颗宝石？

第一轮

Agent 1：设 x 为红宝石的数量。那么钻石的数量是175，红宝石比钻石少35颗。因此 x = 175 - 35。翡翠的数量是红宝石数量的两倍，即 2x。

计算宝石的总数：总宝石数 = 175 + x + 2x = 3x + 175。

我们不知道确切的 x 值，但我们知道它表示红宝石的数量，且红宝石的数量比钻石少35颗，即 x < 175。我们可以试一些值：当 x = 50 时，总宝石数为 3(50) + 175 = 325；当 x = 100 时，总宝石数为 3(100) + 175 = 475。所以答案应该更接近175颗钻石。通过反复尝试，我们发现当 x = 40 时，总宝石数为3(40) + 175 = 295。

结果不正确（红叉）。

Agent 2：如果钻石有175颗，那么红宝石的数量是比钻石少35颗，因此红宝石的数量为140颗。翡翠是红宝石的两倍，即2 × 140 = 280颗翡翠。

计算总宝石数量：175 + 140 + 280 = 595。因此，宝箱里共有595颗宝石。

结果正确（绿勾）。

第二轮

Agent 1：根据其他代理的解决方案，我们有两个答案：一个代理认为红宝石数量是40，总宝石数量为225。另一个代理认为红宝石数量是140，总宝石数量为595。

我们知道红宝石的数量比钻石少35颗，所以红宝石数量为175 - 35 = 140，与第二个代理的结果一致。另一个认为总共有225颗宝石的代理假设翡翠的数量是红宝石数量的两倍，而非红宝石数量的两倍。使用此假设，我们得出红宝石数量为140，翡翠数量为2 × 140 - 35 = 245，因此总宝石数为175 + 140 + 245 = 560。最后的答案是560。

结果不正确（红叉）。

Agent 2：在回顾其他代理的解决方案后，我同意第二个代理的结论，即红宝石的数量为140，总宝石数量为595。因此，我的答案是595。

结果正确（绿勾）。

第三轮

Agent 1：在回顾其他代理的解决方案后，我同意第二个代理的结论，即红宝石的数量为140，总宝石数量为595。因此，我的答案是595。

结果正确（绿勾）。

Agent 2：在回顾其他代理的解决方案后，我也同意第二个代理的结论，即红宝石的数量为140，总宝石数量为595。因此，我的答案也是595。

结果正确（绿勾）。）

1、原理

Language Generation through Multiagent Debate是一种通过多代理辩论的方式来生成语言的模型架构

1. 多代理生成答案：模型中存在多个语言代理（或称为多个模型实例），每个代理在面对相同的问题时，独立生成自己的答案。每个代理代表了不同的思路或信息来源。

2. 相互批判与辩论：每个代理不仅生成自己的答案，还会审阅和批判其他代理的回答。代理在评估他人回答的过程中不断修正自己的答案，并且这种修正过程会持续多个回合。

3. 答案共识：通过多回合的辩论，代理们会逐渐趋向于一致的答案。在这个过程中，如果某些事实不确定，代理们会有分歧，最终的答案会通过不断排除不确定性而变得更为准确。

4. 提高推理与事实准确性：这种方法旨在解决当前语言模型存在的“幻觉”问题，即模型会错误地生成事实或推理过程。通过代理之间的相互辩论，可以减少这种错误并提升答案的可靠性。

5. 应用场景：该方法适用于多种推理和事实验证任务，如数学问题、历史传记生成、国际象棋棋步预测等。在这些场景中，多代理辩论的机制比单一代理生成的答案更加精确和可信。

该方法的优点是它不需要对模型内部的信息（如梯度或概率）进行访问，只需对生成的语言结果进行黑盒操作即可应用。此外，它也能与其他提升语言模型的方法，如零样本推理（zero-shot chain-of-thought reasoning），结合使用以进一步提高性能。

Du Y, Li S, Torralba A, et al. Improving factuality and reasoning in language models through multiagent debate[J]. arXiv preprint arXiv:2305.14325, 2023.

MIT CSAIL

Google Brain

----------------------------

03.Progressive-hint prompting improves reasoning in large language models

渐进式提示提示法提高了大型语言模型的推理能力

摘要：大型语言模型（LLMs）在推理任务中的表现在很大程度上依赖于提示设计，其中“思维链”（Chain-of-Thought, CoT）和自一致性是提升该能力的重要方法。然而，这些方法并没有充分利用LLM生成的答案来指导后续的响应。本文提出了一种新的提示方法，称为逐步提示（Progressive-Hint Prompting, PHP），它通过使用先前生成的答案作为提示，逐步引导模型接近正确答案，允许用户与LLM之间进行多次自动交互。PHP方法与CoT和自一致性互不冲突，因此可以轻松与最先进的技术结合，进一步提高性能。我们在七个基准数据集上进行了广泛的实验，结果表明，PHP显著提升了准确率，同时保持了很高的效率。例如，在使用text-davinci-003模型时，与复杂的CoT相比，PHP在GSM8K数据集上的贪婪解码表现提升了4.2%，而在使用自一致性时，路径样本量减少了46.17%。通过结合GPT-4和PHP，我们在SVAMP（89.1% → 91.9%）、GSM8K（92% → 95.5%）、AQuA（76.4% → 79.9%）和MATH（50.3% → 53.9%）数据集上实现了当前最好的表现。

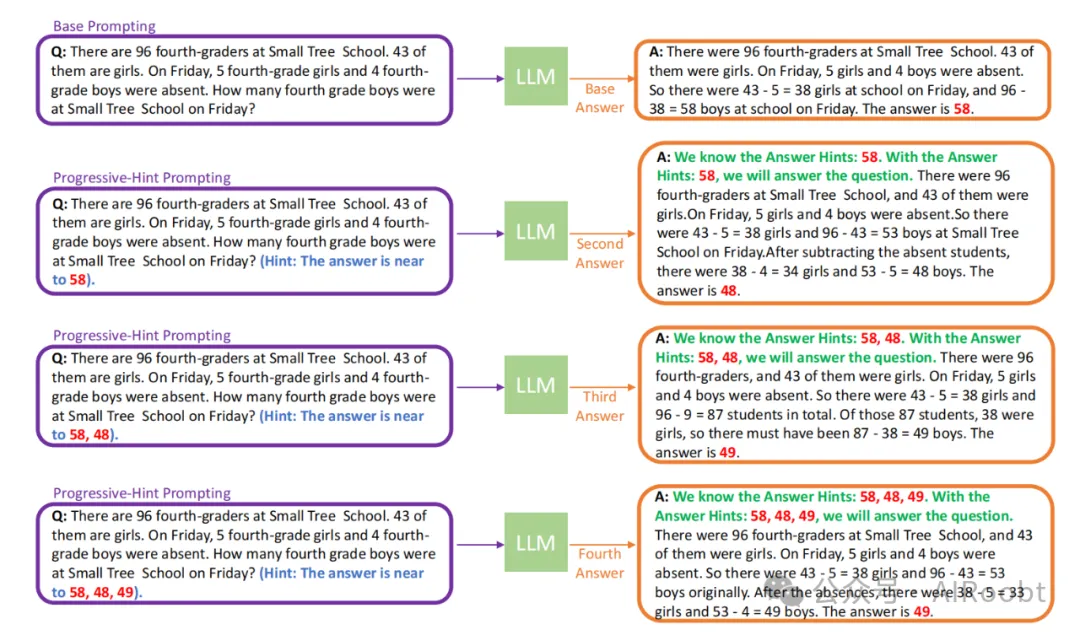
图3 我们提出的逐步提示法结合了生成的答案和问题，用于双重检查，分为两个阶段。在第一阶段，我们通过将当前问题和基础提示（如思维链提示或复杂思维链提示）结合起来，生成基础答案。在第二阶段，我们通过相应的逐步提示提示生成后续答案，例如逐步提示思维链（PHP-CoT）或逐步提示复杂思维链（PHP-Complex CoT）。当两次连续的答案相同时，交互停止。- 紫色框：LLM的输入。 - 橙色框：LLM的输出。

（图片内容：

Base Prompting（基础提示）

问题：小树学校有96名四年级学生，其中43名是女生。星期五，5名四年级女生和4名四年级男生缺席。星期五有多少名四年级男生在小树学校？

LLM（大型语言模型）回答：小树学校有96名四年级学生，其中43名是女生。星期五，5名女生和4名男生缺席。所以，星期五学校里有43 - 5 = 38名女生，96 - 38 = 58名男生。答案是 58。

Progressive-Hint Prompting（逐步提示法）

问题：小树学校有96名四年级学生，其中43名是女生。星期五，5名四年级女生和4名四年级男生缺席。星期五有多少名四年级男生在小树学校？（提示：答案接近58）。

LLM回答：我们知道答案提示是58。基于这个提示，我们将重新回答问题。小树学校有96名四年级学生，其中43名是女生。星期五，5名女生和4名男生缺席。所以，星期五学校里有43 - 5 = 38名女生，96 - 43 = 53名男生。减去缺席的学生后，有38 - 4 = 34名女生和53 - 5 = 48名男生。答案是 48。

Progressive-Hint Prompting（逐步提示法）

问题：小树学校有96名四年级学生，其中43名是女生。星期五，5名四年级女生和4名四年级男生缺席。星期五有多少名四年级男生在小树学校？（提示：答案接近58，48）。

LLM回答：我们知道答案提示是58和48。基于这些提示，我们将重新回答问题。小树学校有96名四年级学生，其中43名是女生。星期五，5名女生和4名男生缺席。所以，星期五学校里有43 - 5 = 38名女生，96 - 9 = 87名学生。这87名学生中有38名是女生，所以应该有87 - 38 = 49名男生。答案是 49。

Progressive-Hint Prompting（逐步提示法）

问题：小树学校有96名四年级学生，其中43名是女生。星期五，5名四年级女生和4名四年级男生缺席。星期五有多少名四年级男生在小树学校？（提示：答案接近58，48，49）。

LLM回答：我们知道答案提示是58、48、49。基于这些提示，我们将重新回答问题。小树学校有96名四年级学生，其中43名是女生。星期五，5名女生和4名男生缺席。所以，原本有43 - 5 = 38名女生和96 - 43 = 53名男生。缺席之后，有38 - 5 = 33名女生和53 - 4 = 49名男生。答案是 49。）

1、原理

Progressive-Hint Prompting (PHP) 是一种通过逐步利用模型之前生成的答案提示，来引导模型逐渐接近正确答案，从而提升大型语言模型（LLMs）推理能力的方法。这个过程涉及用户与模型之间的多次交互，每次生成的答案都会作为提示用于下一次的提示输入，逐步优化模型的推理过程。

PHP 的关键部分包括：

1. 基础答案：模型首先使用基础提示（如 Chain-of-Thought 或 Complex CoT）生成初始答案，这个答案是进一步推理的起点。

2. 提示引入：将基础答案作为提示，用于后续的交互中。模型通过重新审视问题，并结合该提示，逐步改进推理过程，获得更准确的答案。

3. 逐步优化：这个过程会一直持续，直到模型生成的两个连续答案相同，这表示模型找到了稳定的解决方案。

4. 类似人类的思维过程：该方法模拟了人类的思维过程，利用之前的答案不断检查和修正错误，最终得到更精确的结果。

PHP 能有效提升模型在多步骤推理任务中的表现，尤其是在数学和逻辑推理等场景中。

2、图片注释

问题：

“小树学校有96名四年级学生，其中43名是女生。星期五，5名四年级女生和4名四年级男生缺席。星期五有多少名四年级男生在学校？”

传统解答：

模型最初生成的答案可能是：

- 总共有96名四年级学生，其中43名是女生。5名女生缺席，所以学校有43 - 5 = 38名女生在校。学校总共有96 - 38 = 58名男生在校。

- 答案是58。

使用 PHP 进行提示优化：

1. 在第一次模型生成答案后，我们将“58”作为提示，再次询问模型：

- “我们知道答案提示是58。通过这个提示重新回答问题。” 模型这次可能会重新计算，并提供一个不同的答案：

- 答案是48（因为它意识到计算错误，男生数量应该是53，减去缺席的4名男生）。

2. 接着，我们将这两个答案（58和48）作为新的提示进行第三次推理：

- “我们知道答案提示是58和48。通过这些提示重新回答问题。” 模型可能进一步调整推理：

- 答案是49。

3. 最后，通过不断提供提示，模型逐步调整自己的推理过程，直到给出最终稳定的答案。

通过这种逐步引导，模型能够修正最初的错误推理，从而得出更准确的答案。这展示了 PHP 如何通过利用之前的答案提示逐步优化推理过程，使得模型能够更接近正确的解答。

Zheng C, Liu Z, Xie E, et al. Progressive-hint prompting improves reasoning in large language models[J]. arXiv preprint arXiv:2304.09797, 2023.

Chinese University of Hong Kong

Huawei Noah’s Ark Lab

​

本文转载自公众号AIRoobt ，作者：AIRoobt

原文链接：​​https://mp.weixin.qq.com/s/teWkXNT_7mDDgvSKGd5YNg​​