巧妙应用机器学习引导科研理解

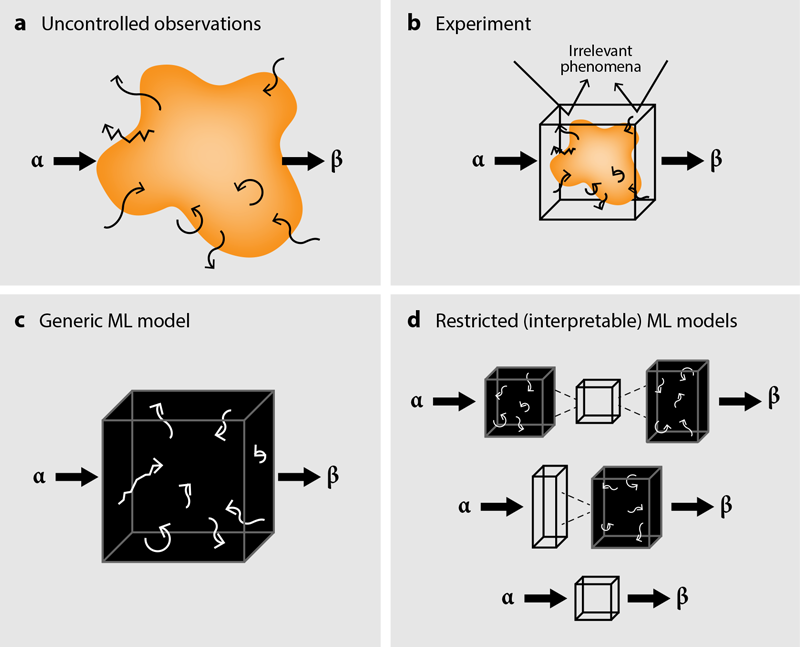
图1：理解物理现象的途径有很多，其中原因α产生结果β。(a) 不受控制的观察会导致原因和结果之间的松散联系。(b) 结合已知物理定律的精心设计的实验可以得到简单的因果关系，但为复杂现象设计这样的实验可能极具挑战性。(c) 通用的机器学习（ML）模型（神经网络）通过优化许多参数来拟合复杂数据，但解析这些黑箱（例如，数百万个）参数的意义是非常困难的。(d) 包含一些限制或简化操作（白色）的机器学习模型使得识别复杂现象的因果链的某些方面成为可能，从而指导模型构建或进一步实验。  

物理理论和机器学习（ML）模型都依赖于其在未见情境下预测结果的能力。然而，对于前者的要求要高得多。要成为被接受的知识，理论必须符合已知的物理定律——而且，至关重要的是，必须是可解释的。

一个可解释的理论能够解释现象为何发生，而不仅仅是预测其形式。拥有这样的解释可以指导新理论的范围，使其能够在新的背景下应用，同时也将其与先前的知识联系起来并纳入其中。

迄今为止，研究人员在使ML模型（或任何自动化优化过程）产生符合这些标准的新理论方面仍然存在很大困难。

芝加哥大学的乔纳森·科伦和文琴佐·维泰利及其同事现在展示了成功地利用ML的方式——不是作为研究人员的替代者，而是作为指导者，帮助构建复杂系统的模型[1]。在他们方法的演示中，研究人员发现了一个先前被忽视的项，推进了对流体系统动力学的更全面理解。

为了建立新模型，物理学家通常在受控实验中观察现象（图1a），并尝试用方程将系统的参数相互关联（图1b）。然后，通过直觉和试错的组合，物理学家们修改实验、理论或两者同时修改，直到找到一组描述数据的方程。

先前的知识——例如，系统应该没有历史依赖，温度是均匀的，或忽略重力——大大缩小了可能的解决方案和所需实验探索的范围。这种范围的大幅度缩小通常是必要的，因为我们发现人类很难处理超过屈指可数几个维度的问题。

相比之下，ML模型在给定（非常）高维空间进行探索时能找到更准确且更具普遍性的解决方案[2]。这些模型优化大量可调参数，直到其预测与数据匹配。不幸的是，通用ML模型找到的解决方案通常过于复杂且方法依赖性强，难以提取“为什么”[3]。

因此，应用这些方法的研究人员往往局限于不能令人满意的说法，即他们的数据包含预测信息[4]。然而，这些信息是什么以及为什么具有预测性，仍然隐藏在众多杂乱变量的黑箱中（图1c）。

识别数据中预测信息所在的技术正在出现[5]，但在科学过程中很少使用。复杂ML模型的替代方案是使用算法直接搜索可能方程的库来描述系统[6]。

然而，这种策略随着系统复杂性的增加而效果不佳，使其在现在科研关注的现象中难以应用。将ML融入一般发现过程中需要平衡：方法应具有足够的自由度以发挥其潜力，同时结果所在的领域也应受到限制，以便结果可解释。

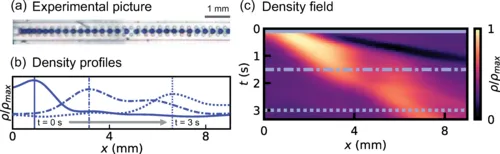
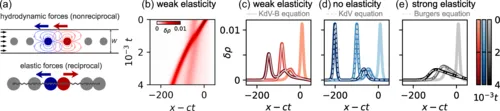
科伦、维泰利及其同事正是通过一系列ML算法实现了这一点[1]。他们的工作集中在流体力学中的一个范例问题上：微流体通道中水滴的单排队列，悬浮在另一种流体中，这使它们相互作用并形成传播的冲击前沿。该系统以前通过一个描述流体密度变化的偏微分方程建模。

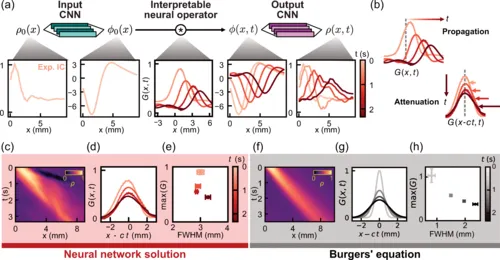
但这个方程（称为伯格斯方程），未能捕捉系统动力学的关键方面。为了揭示缺失的物理学，研究人员首先训练一个ML模型来预测一维水滴密度场ρ的时间演变——换句话说，他们让算法找到一个函数M，使初始密度ρ0随时间演进：M[t,ρ0]=ρ(t)。

为了使他们的模型具有可解释性，研究人员将其构建为三个连续操作的组合。

首先，一个神经网络 N 将密度转换为一个新的1D场，他们称之为 φ0=N[ρ0]。虽然这个“潜在”场没有容易解释的物理意义，它仅包含有关初始密度场的信息。

其次，将这个场输入到一个称为 F 的函数中，该函数使其随时间推进——换句话说，F(φ0,t)=φ(t)。研究人员将 F 的形式限制为一组线性操作。

最后，这个场通过另一个神经网络转换回密度，基本上是第一个步骤的逆过程。（从数学上讲，整个过程可以描述为 M[t,ρ0]=N−1[F(t,N[ρ0])]=ρ(t) ，如图1d上方所示）。通过同时优化这三个步骤以匹配实验数据，研究人员发现比伯格斯方程更好的预测结果。 

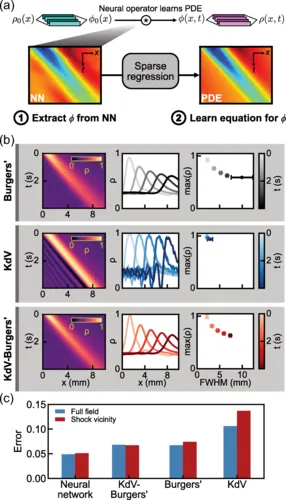
随后，研究人员利用一种算法来寻找数值函数的简化分析逼近[6]。对于一个在实验数据上训练的典型的神经网络，这一步骤通常会失败（图1c）。

但值得注意的是，它产生了一个包含五个项的线性偏微分方程，作为 F 的良好替代。尽管这个方程作用于（不可解释的）潜在变量 φ0，但 F 作为时间传播者的角色使得每一项的意义在高层次上是可以理解的。

具体来说，研究人员将其中一个微分项与色散相关联——即流体波速的频率依赖性。这样的色散项在伯格斯方程中并不存在，但团队发现其加入能更准确地描述水滴密度场中出现的冲击前沿动力学。

最后，团队开发了一个相互作用水滴的模型，发现这个新增的色散项是非对称流体动力学相互作用的直接结果。

这项工作提供了一个令人兴奋的机器学习（ML）应用，它在科学探索中充当了罗盘，这需要一种根本不同于标准ML实践的方法，后者主要通过预测准确性来评判模型。然而，对于科学探索来说，“最佳”模型是那些能够提供物理洞察（即“为什么”）的模型，即使它们可能不是最准确的。

事实上，团队发现添加关键的色散项实际使预测误差略微增加，相比之下，其他ML模型在相同问题上的应用误差较低；然而，这一色散项清楚地捕捉了冲击前沿附近缺失的物理现象。正是通过连续模型的闭环并识别这一色散项的来源，科伦、维泰利及其同事才能巩固他们的结论。

这一工作流程与宾夕法尼亚大学近期使用ML作为实验指南的工作相呼应[7]，在这些工作中，训练预测颗粒材料堵塞的最简单和“最弱”（最不具预测性）的模型提供了最深刻的见解，并提升实验验证了他们的解释。   

计算能力的提升极大地加快了科学数据分析，但我们对这些数据的探索通常仍完全由人类驱动。随着物理学家研究日益复杂的涌现现象，潜在物理模型的维度、以及所需实验探索的复杂性迅速增长。

虽然标准分析工具允许我们识别可靠的趋势，但在（必然）杂乱的数据中追踪高度非线性、历史依赖和多尺度效应可能不切实际，除非有一个能够同时处理100维数据的指南。研究这些现象，可能需要对学科内容和ML工具的熟练掌握，这既可以作为实验指导，也可以作为理论指导。

参考文献

1. J. Colen et al., “Interpreting neural operators: How nonlinear waves propagate in nonreciprocal solids,”Phys. Rev. Lett. 133, 107301 (2024).
2. J. W. Rocks and P. Mehta, “Memorizing without overfitting: Bias, variance, and interpolation in overparameterized models,”Phys. Rev. Res. 4, 013201 (2022).
3. C. Rudin et al., “Interpretable machine learning: Fundamental principles and 10 grand challenges,”Statist. Surv. 16, 1 (2022).
4. S. Dillavou et al., “Beyond quality and quantity: Spatial distribution of contact encodes frictional strength,”Phys. Rev. E 106, 033001 (2022).
5. K. A. Murphy and D. S. Bassett, “Information decomposition in complex systems via machine learning,”Proc. Natl. Acad. Sci. U.S.A. 121, 13 (2024).
6. S. L. Brunton et al., “Discovering governing equations from data by sparse identification of nonlinear dynamical systems,”Proc. Natl. Acad. Sci. U.S.A. 113, 3932 (2016).
7. J. M. Hanlan et al., “Cornerstones are the key stones: Using interpretable machine learning to probe the clogging process in 2D granular hoppers,”arXiv:2407.05491.

本文转载自​​清熙​​，作者： 萨姆 ​​​​