解密GCN,手把手教你用PyTorch实现图卷积网络
图神经网络(GNNs,Graph Neural Networks)是一类专为图结构数据设计的强大神经网络,擅长捕捉数据之间的复杂联系和关系。
相较于传统神经网络,GNN在处理相互关联的数据点时更具优势,比如在社交网络分析、分子结构建模或交通系统优化等领域,GNN能够发挥出卓越的性能。
1 GNN概述
图神经网络是近年来新兴的一类深度学习模型,擅长处理图形数据。
传统神经网络处理的是像数字列表这样的简单数据,而图神经网络能处理更复杂的图形数据,比如由很多点(称为节点)和连接这些点的线(称为边)组成的图形,并且能从这些图形中找出重要的信息。
其核心机制是让图中的每个节点通过与邻近节点的信息交换,来学习自己在整体图形中的位置和特性。这种基于信息传递的方法,让图神经网络能够快速捕捉到图形里的结构和关系。
这种技术在很多领域都大放异彩,比如社交网络分析、分子结构预测、知识图谱构建等等。
随着科学家们不断地研究和创新,图神经网络也在蓬勃发展,衍生出多种新模型,为机器学习在图形数据领域的应用开辟了新的可能性。
2 图卷积网络(Graph Convolutional Networks)
简单来说,图卷积网络(GCN)跟传统神经网络一样,是由多层结构堆叠而成的。
在深度学习中,图卷积网络(GCN)的核心是图卷积层,其工作机制与卷积神经网络(CNN)的卷积层颇为相似。
在CNN中,卷积层负责捕捉图像中局部区域的像素信息,这个过程称之为“感受野”(Receptive Field),通过它,我们可以提取出图像的简化和低维特征。
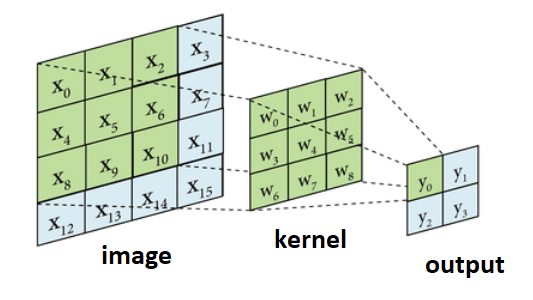
GCN层的工作原理与之类似,不过不是处理像素,而是处理图中的节点信息。它通过收集每个节点及其相邻节点的信息,来构建节点的表示,从而捕捉图中的结构特征。
3 推导GCN方程式
来聊聊图卷积网络(GNN)的数学原理。
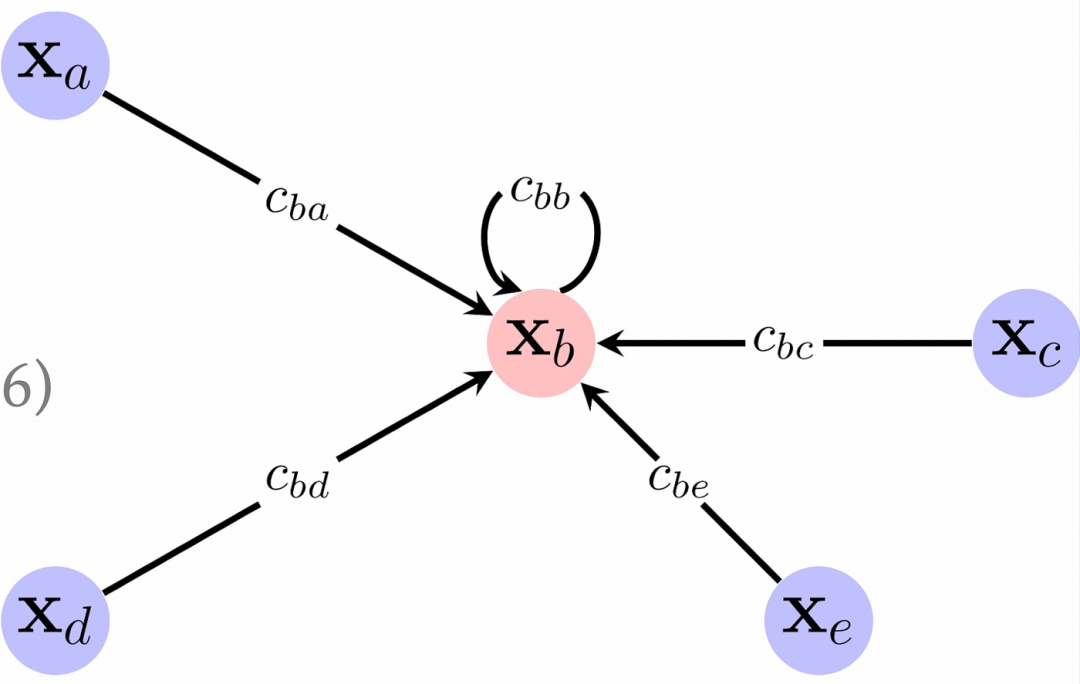
首先,GNN的输入是一个图,这个图可以用节点特征的矩阵和邻接矩阵来表示。邻接矩阵里的1代表两个节点之间有连接,0则表示没有连接。

这个例子的邻接矩阵是这样的:
节点 1 -- 节点 2
|
节点 3当我们用A乘以节点特征矩阵X,得到的结果是每个节点的邻居对每个特征的贡献总和。简单来说,就是把每个节点i的邻居j的特征加起来:
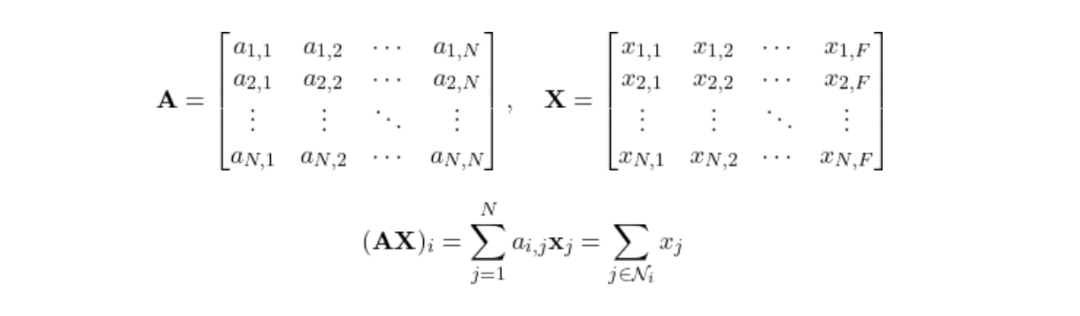
然而,我们不应忽视节点自身的特征。为了将节点自身的特征也考虑进来,可以在邻接矩阵A的对角线上增加1,这在数学上相当于引入了单位矩阵I。
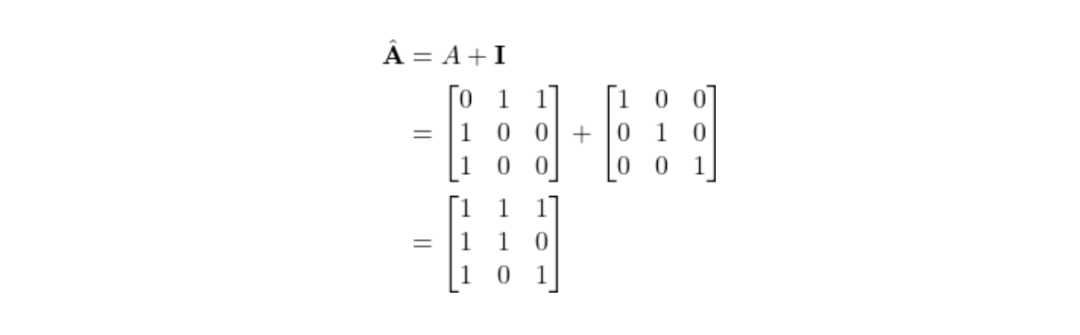
这样:
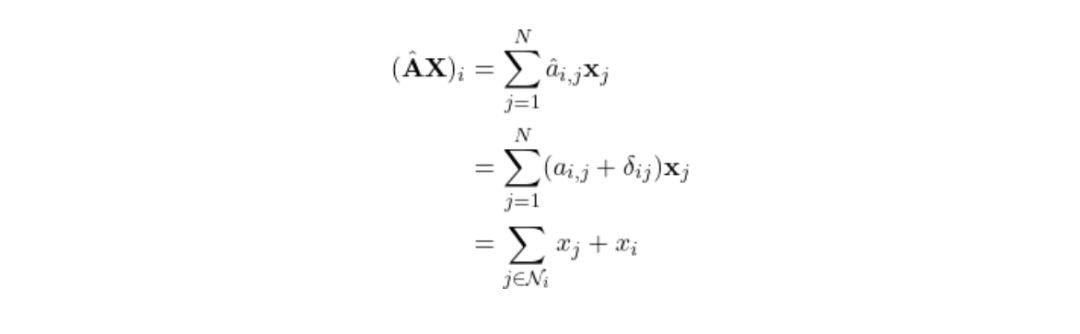
但是,还有一个问题:节点的邻居数量可能不一样。有的节点有几百个邻居,有的可能只有一两个。为了公平起见,我们需要对总和进行归一化。
一种方法是用每个节点的邻居数(也就是节点的度)来除以这个总和。可以创建一个对角线上是节点度的对角度矩阵D,然后归一化方程:
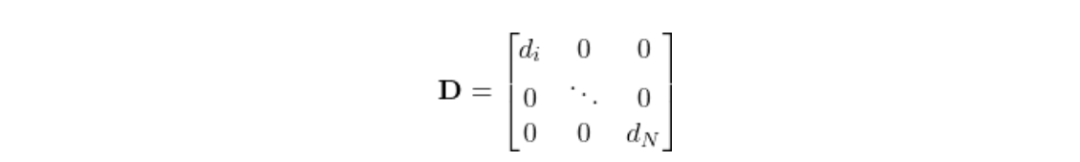
这样:
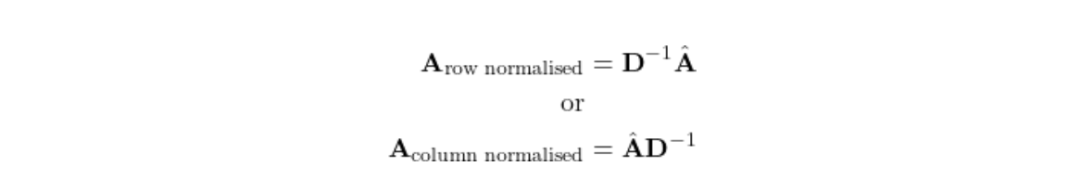
直观地说,行归一化就是取邻居特征的平均值,而列归一化则考虑了邻居的邻居数。
为了两者兼顾,采用对称归一化:
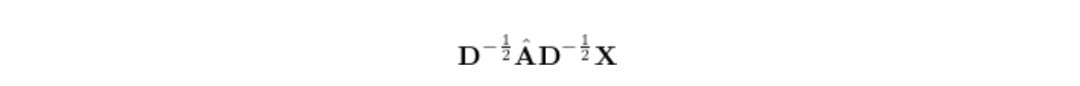
这考虑了当前节点的邻居数和邻居的邻居数。
这样一来,我们的方程式就越来越完整了!
最后,我们需要一些参数来训练机器学习模型,就像在线性回归中那样,可以简单地插入一个权重矩阵。
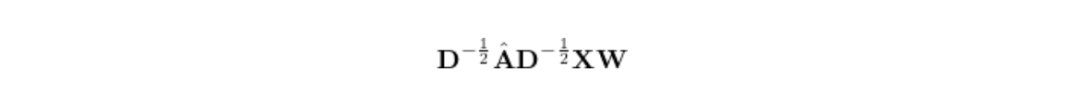
而且,我们知道添加非线性可以提供更好的特征表示,所以还可以在上面加一个ReLU激活函数。
最后:
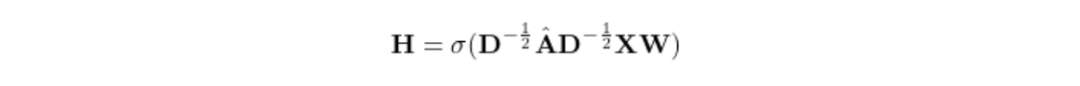
4 PyTorch 实现
接下来,看看如何在 PyTorch 中实现图卷积网络。
首先,在类的初始化方法__init__中,我们会设置好邻接矩阵A、度矩阵D和权重矩阵W。
然后,在模型的前向传播过程中,利用这些组件来构建节点的新特征矩阵H。
import torch
import torch.nn as nn
import torch.nn.functional as F
class GCNLayer(nn.Module):
"""
GCN 层
参数:
input_dim (int): 输入的维度
output_dim (int): 输出的维度(softmax 分布)
A (torch.Tensor): 2D 邻接矩阵
"""
def __init__(self, input_dim: int, output_dim: int, A: torch.Tensor):
super(GCNLayer, self).__init__()
self.input_dim = input_dim
self.output_dim = output_dim
self.A = A
# A_hat = A + I
self.A_hat = self.A + torch.eye(self.A.size(0))
# 创建对角度矩阵 D
self.ones = torch.ones(input_dim, input_dim)
self.D = torch.matmul(self.A.float(), self.ones.float())
# 提取对角元素
self.D = torch.diag(self.D)
# 创建一个新张量,对角线上是元素,其他地方是零
self.D = torch.diag_embed(self.D)
# 创建 D^{-1/2}
self.D_neg_sqrt = torch.diag_embed(torch.diag(torch.pow(self.D, -0.5)))
# 初始化权重矩阵作为参数
self.W = nn.Parameter(torch.rand(input_dim, output_dim))
def forward(self, X: torch.Tensor):
# D^-1/2 * (A_hat * D^-1/2)
support_1 = torch.matmul(self.D_neg_sqrt, torch.matmul(self.A_hat, self.D_neg_sqrt))
# (D^-1/2 * A_hat * D^-1/2) * (X * W)
support_2 = torch.matmul(support_1, torch.matmul(X, self.W))
# ReLU(D^-1/2 * A_hat * D^-1/2 * X * W)
H = F.relu(support_2)
return H
if __name__ == "__main__":
# 示例用法
input_dim = 3 # 假设输入维度是 3
output_dim = 2 # 假设输出维度是 2
# 示例邻接矩阵
A = torch.tensor([[1., 0., 0.],
[0., 1., 1.],
[0., 1., 1.]])
# 创建 GCN 层
gcn_layer = GCNLayer(input_dim, output_dim, A)
# 示例输入特征矩阵
X = torch.tensor([[1., 2., 3.],
[4., 5., 6.],
[7., 8., 9.]])
# 前向传递
output = gcn_layer(X)
print(output)
# tensor([[ 6.3438, 5.8004],
# [13.3558, 13.7459],
# [15.5052, 16.0948]], grad_fn=<ReluBackward0>)本文转载自 AI科技论谈,作者: AI科技论谈

















