语言模型的神秘面纱：小学数学与隐含推理过程

一、结论写在前面

论文标题：Physics of Language Models: Part 2.1, Grade-School Math and the Hidden Reasoning Process

论文链接：​​https://arxiv.org/pdf/2407.20311​​

预览页面 - 视频：​​https://physics.allen-zhu.com/part-2-grade-school-math/part-2-1​​

语言模型的最新进展展示了其在解决数学推理问题上的能力，达到了接近完美的准确率，如GSM8K等小学水平数学基准测试。

论文研究了语言模型如何解决这些问题。论文设计了一系列控制实验来回答几个基本问题：    

(1) 语言模型是否真的发展了推理技能，还是仅仅记忆了模板？

(2) 模型的隐含（心理）推理过程是什么？

(3) 模型解决数学问题所用的技能与人类相似还是不同？

(4) 模型在GSM8K类数据集上训练后，是否发展了超出解决GSM8K问题所需的推理技能？

(5) 导致模型推理错误的心理过程是什么？

(6) 模型需要多大或多深才能有效解决GSM8K级别的数学问题？

论文通过合成设置展示了语言模型能够通过真正的泛化来解决小学数学问题，而不是依赖于数据污染或模板记忆。论文开发了探测技术来检查模型的隐藏推理过程。论文的发现揭示了这些模型能够学习与人类认知过程一致的数学技能，以及训练数据中不存在“新的思维过程”。

此外，论文提出了一种方法，在模型开始解决问题之前预测其错误，并解释模型为何在发生错误时犯错。基于这一发现，论文撰写了一篇单独的论文，以提高语言模型的数学推理准确性。论文还提供了一种原则性的方法，将模型的深度与其推理能力相连接。相比于推动数学基准，论文相信这项研究为从不同角度研究语言模型的数学推理技能打开了大门。

总结如下：

•结果2。论文证明，预训练于论文合成数据集的GPT2模型，不仅在解决同分布数学问题上达到99%的准确率，还能泛化到未见过的分布，例如推理长度超过训练中任何样本的问题。这与算术中的长度泛化类似，但在论文的案例中，模型从未见过与测试时相同长度的训练样本。这表明模型真正学会了某些推理技能，而非记忆解题模板。

•结果3：关键在于，模型能够学会生成最短的解决方案，几乎总是避免不必要的计算。这表明模型在生成之前会制定一个计划，以避免计算任何对解决基础数学问题无用的量。

•结果4：论文通过探针检查模型的内部状态，引入了六个探针任务来阐明模型如何解决数学问题。例如，论文发现模型在开始生成之前预处理了所有必要的参数。同样，人类也会进行这种预处理，尽管论文通常会将其写下来。    

•结果5：令人惊讶的是，模型在预训练后还学会了不必要但重要的技能，如全对依赖。在提出任何问题之前，它已经以高准确度计算了哪些参数依赖于哪些参数，即使其中一些对解决数学问题并不需要。值得注意的是，计算全对依赖是一项技能，不需要用于拟合训练数据中的所有解决方案。据论文所知，这是首次证据表明，语言模型能够学习超越其预训练数据所需的有用技能。这可能是AGI中“G”（通用）的初步信号来源。

•结果6：论文解释了错误发生的原因。例如，模型会犯系统性错误，这些错误可以通过探查其内部状态来解释。有时，这些错误在模型生成答案之前就可以预测，使它们独立于随机生成过程。论文将此与实践联系起来，指出GPT-4/4o也会犯类似的错误（尽管论文无法探查它们的内部状态）。

•结果 7+8 。语言模型的深度对其推理能力至关重要。例如，一个16层、576维的transformer比一个4层、1920维的transformer解决更复杂的问题（在推理长度上），尽管后者体积是前者的两倍。即便使用思维链（Chain-of-Thought, CoT）也是如此。论文通过所涉及的心理过程的复杂性来深入解释这种必要性。论文主张使用受控的、合成的数据作为一种更有原则的方法来得出这样的结论，这与基于使用互联网预训练数据的训练损失得出的"只有规模才重要"等预测形成对比[14]。

虽然论文不会过分夸大地声称论文的发现直接适用于像GPT-4这样的基础模型或更具挑战性的数学推理任务，但论文相信论文的工作显著推进了对语言模型如何发展其数学推理能力的理解，而这必须以一种不同于推动基准测试的方式来完成。

二 论文的简单介绍

2.1 论文的背景

语言模型领域近年来取得了显著进展。大型模型如GPT-4已显示出初步的通用智能迹象 ，而较小的模型则通过解决具有挑战性的编码和数学问题展示了良好的推理能力。    

论文聚焦于小型语言模型解决小学数学问题的能力。与先前工作通过实证方法提升模型在小学数学基准测试（如GSM8K 及其扩展版本）上的准确率不同，论文采取了一种更为原则性的方法。论文的目标是理解以下基本问题：

1.语言模型如何学会解决小学水平的数学问题？它们是否仅仅记忆了模板，还是学会了类似于人类的推理技能？或是它们发现了新的解题技巧？

2.仅在小学数学问题上训练的模型是否仅学会了这些问题的解决方法，还是它们发展出了某种更普遍的智能？

3.语言模型在解决小学数学问题时可以有多小？深度（层数）是否比宽度（每层神经元数）更重要，还是如从业者所建议的那样，只有模型的大小才是关键 ？

这些问题对于理解语言模型的智能至关重要。为了研究它们，似乎很自然地会考虑从预训练模型开始，并在现有数据集（如GSM8K或GPT-4增强版数据集）上进行微调。然而，这种方法存在显著局限性：

•数据污染。现有模型的预训练数据大多来自公开可用的互联网，这些数据杂乱无章。论文无法知晓其中包含了多少数学问题及其结构。关于GSM8K基准测试是否已泄露至语言模型的训练数据集中存在重大疑虑 。即便确切数据未泄露，预训练模型可能已经见过几乎相同的问题（例如，同一问题但数字不同）。因此，这种方法无法解答问题1至3。论文无法确定模型是否真正学会了推理技能，或者它只是在训练过程中记忆了问题模板。因此，论文需要完全控制模型的预训练数据，并必须从头开始训练语言模型。这一点在近期文献 [ 2, 3 ] 中已被反复强调。

•解题多样性。现有的微调数据，如GSM8K训练集，仅包含7.5千道小学数学题，不足以从头开始训练模型。尽管近期工作使用GPT-4扩充GSM8K，但这仍无法满足论文的需求。GPT-4扩充的问题可能偏向于少数解题模板，因为原始GSM8K数据中的解题模板非常有限（显然，最多8千个）。论文需要一个更大、更多样的小学数学题集合。

基于这些考虑，论文提出一个框架，用于生成大量多样的小学数学（GSM）问题，并利用该数据集从头开始训练和测试类似GPT2的语言模型。在该框架中，论文专注于小学数学问题中的“逻辑推理”部分，这涉及问题陈述中参数的依赖关系，例如“爱丽丝的苹果是鲍勃的橙子和查尔斯的香蕉总和的三倍”。论文使用合成句子来降低因常识带来的难度，例如“一支蜡烛以每小时1英寸的速度燃烧了12小时”（暗示蜡烛在缩短）。论文还消除了纯算术的难度：论文仅考虑整数和算术模23。    

此外，论文的框架确保生成的数学问题高度多样，不来自少数模板。即使忽略所有算术、英语、变量名称和未使用的参数，论文的问题仍拥有超过90万亿种解题模板（见命题2.2），远超GPT2-small（1亿参数）的规模。因此，语言模型无法通过简单记忆解题模板来解决论文的问题。

论文使用GPT2模型，但将其位置嵌入替换为旋转位置嵌入（positional embedding with rotary embedding，RoPE）。为了简洁，论文仍称其为GPT2。

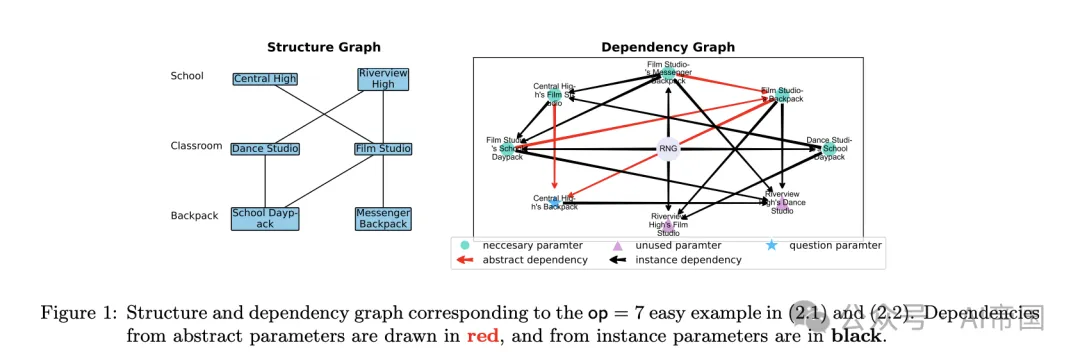
图1：对应于 (2.1) 和 (2.2) 中 op=7 简单示例的结构和依赖关系图。抽象参数的依赖关系以红色绘制，实例参数的依赖关系以黑色绘制

2.2 结果1：数据生成

动机。回想一下GSM8K数据集中的一个标准小学数学问题：

Betty正在为一个新的钱包存钱，这个钱包花费100。Betty只有她所需钱的一半。她的父母决定为此目的给她15，而她的祖父母给她的钱是父母的两倍。Betty还需要多少钱才能买这个钱包？

这个问题涉及多个参数，这些参数的值通过各种等式相互关联，例如“Betty目前的钱 = 0.5 × 钱包的成本”和“祖父母给的钱 = 2 × 父母给的钱”。受此启发，论文通过一个捕捉参数依赖关系的合成生成管道构建了一个类似GSM8K的数学数据集。论文希望至少捕捉以下三种类型的依赖关系。

•直接依赖：例如 A=5×(X+Y)，因此可以在之后计算    

•实例依赖：例如“每个教室有 X 把椅子，有 Y 个教室。”在这里，模型必须通过将 X 乘以 Y 来推断椅子的总数。

•隐式依赖：例如，“Bob 的水果比 Alice 多 3 倍。Alice 有 3 个苹果、4 个鸡蛋和 2 个香蕉。” 这里，模型必须学习到苹果和香蕉是水果，而鸡蛋不是，并且“Alice 的水果”是一个从问题陈述中派生的抽象参数。

2.2.1 步骤1：图构建与问题生成

层次分类。论文使用一个分层的 categories 结构，每个层次包含可能的项目。例如，categories = (学校, 教室, 背包) 有三个层次；学校类别 = {中央高中, 河景高中, ...}；教室类别 = {舞蹈工作室, 电影工作室, ...}；背包类别 = {学校日包, 信使背包, ...}。论文准备了 4 个预定义的层次分类，每个分类有 4 层，每层包含 100 个项目；这代表了世界知识。

结构图。在每个数学问题中，只有特定的项目存在，导致一个结构图，该图概述了哪些子项目可以在哪些项目下出现，见图 1（左）。例如，

•用一条边连接舞蹈工作室和学校日包表示一个实例参数，“每个舞蹈工作室中的学校日包数量”，这是一个可量化的变量，可以被赋值。这捕获了上述提到的实例依赖。

•抽象参数，如“中央高中教室的总数”，不能被赋值，因此被排除在结构图之外。它们反映了隐式依赖。

依赖图。依赖图是一个有向无环图，它概述了参数之间的依赖关系。对于每个实例参数，论文随机选择一组（最多4个）它可能依赖的参数——可能包括一个代表随机数生成器的特殊顶点RNG。例如，如果"[参数A]比[参数B]和[参数C]的差值多X"，其中X是随机生成的，那么论文就从B、C和RNG到参数A画出边。抽象参数的依赖关系由实例参数的依赖关系隐含表示。这捕捉了上文提到的直接依赖关系(♡)。

问题生成。问题通过用英语描述依赖图来阐述，每个实例参数对应一句话。（抽象参数不描述，因为它们由结构图继承。）论文随机排列句子顺序以进一步增加难度。选择一个参数并在最后（或开始）提问。下面是一个对应于图 1 的简单示例；一个更难的示例在图 11 中。    

2.2.2 步骤 2：解决方案构建（CoT）

设 solution 为一个句子序列，描述解决给定问题所需的步骤，句子按照任何拓扑顺序排列——也称为思维链（Chain-of-Thought, CoT）。对于回答最终问题所需的每个参数，论文从 52 个选择 ( a.. z o r A.. Z ) 中随机分配一个字母，并用一句话描述其计算。

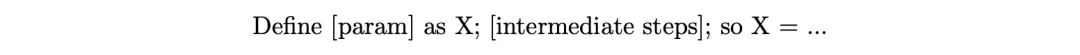
论文考虑模 23 (arithmetics mod 23)的算术以避免涉及大数计算的错误。直接查看一个解决方案示例可能最容易理解，更复杂的示例在图 11 中：

论文强调以下几点：

•解决方案只包含计算最终查询参数所必需的参数。

•解决方案遵循正确的逻辑顺序：即计算中使用的所有参数必须事先出现并被计算。

•论文将计算分解为二元运算：例如，g = 12+13+7 被分解为 g = 12+R 和 R = 13+7，如上述解决方案所示。分号";"的数量等于运算的次数。这降低了解决方案的算术复杂性，而这不是本文的重点。

2.2.3 难度控制

论文在此总结了数据生成过程中使用的主要随机性。这包括随机选择一个层次分类（即英语部分）；一个结构图（即实例参数）；一个依赖图；依赖图上的算术计算；整数（即随机数生成器）；问题句子的排列；以及查询参数。    

论文使用两个参数来控制数据的难度：ip 是实例参数的数量，op 是解决方案操作的数量；数据的难度是这两个参数的递增函数。论文将论文的数据集称为 iGSM，以反映这种合成数据集可以具有无限大小的特性。

2.2.4 训练和测试数据集

论文考虑两类数据集。

•在iGSM-med数据家族中，论文使用ip ≤ 20。

•在iGSM-hard数据家族中，论文使用ip ≤ 28。

此外，论文使用iGSM-med_pq表示将问题放在问题陈述之后，iGSM-med_qp表示相反的顺序（iGSM-hard也类似）。iGSM-med的难度对人类来说已经相当不简单（至少不能通过使用GPT-4/4o进行少样本学习来解决，见图2）。

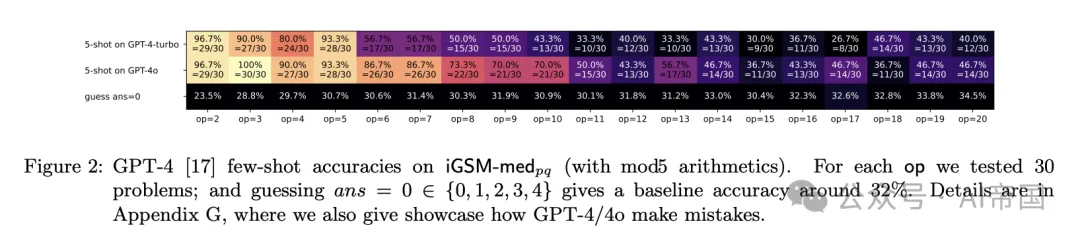
*图2：GPT-4 [17] 在iGSM-medp（含mod5算术）上的少样本准确率。对于每个操作，论文测试了30个问题；

命题2.2. 忽略未使用的参数、数值、句子顺序、英语词汇、a-z和A-Z字母的选择，iGSM-medop=15仍然至少有70亿个解决方案模板，而iGSM-hardop=21至少有90万亿个解决方案模板。

数据污染问题。合成数学数据生成的一个目标是防止互联网数学数据集中的数据污染，如 [22] 所述。虽然可能无法证明基于互联网数据训练的模型完全无污染，但在论文的设置中，论文可以证明这一点：

1.论文进行OOD评估，例如在 op ≥ 28 上，同时仅提供 op ≤ 21 的训练样本。

2.论文使用哈希值小于17（mod 23）的解决方案模板（见脚注 11）进行训练，并使用大于等于17的进行测试。这确保了训练和测试之间在模板级别上没有重叠。    

2.3 结果 2-3：总结模式的行为过程

论文使用 GPT2 架构，但将其绝对位置嵌入替换为旋转位置嵌入，并将其称为 tPT2 以便于分类。论文主要坚持使用 12 层、12 头、768 维的 GPT2（即 GPT2-small）进行实验。论文在 iGSM-med/iGSM-hard 上使用 768/1024 的上下文长度进行预训练，并在评估时使用 2048 的上下文长度。更多细节参见附录 F。

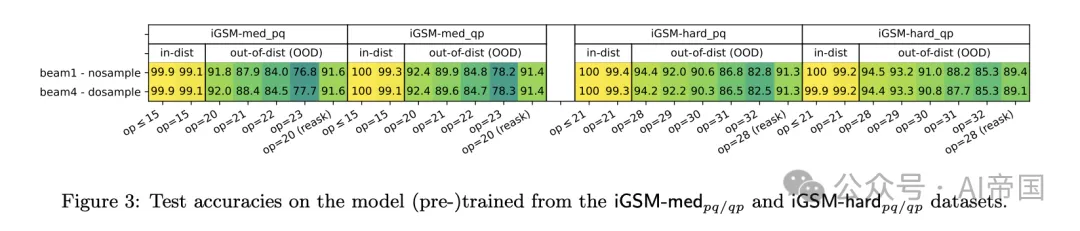
图3：在iGSM-me p q / q p 和 iGSM-hrd 数据集上（预）训练的模型上的测试准确率。

图4：每生成一个正确解决方案所使用的不必要参数/操作数量

结果2：准确性。在充分预训练后，论文给模型一个来自测试集的问题（不含解答），让它继续生成（据称是一个解答followed by一个答案）。由于论文将自己限制在一个固定的解答格式中，语言模型可以轻松学习这种格式，使论文能够编写一个解答解析器来检查解答是否完全正确。

结果2. 图3显示，当使用iGSM-med或iGSM-hard数据预训练时，GPT2表现良好，即使在更难（即更大op）的数学问题上进行分布外评估时也是如此。因此，模型确实可以学习一些推理技能，而不是仅仅记忆解答模板。

这可能让人想起语言模型在算术计算上的长度泛化能力[13, 23]；然而，在论文的案例中，op捕捉了小学数学中的"推理长度"，而论文的模型在测试时从未见过任何与之长度相同的训练样本。

这样的准确率也表明，论文的iGSM数据家族确实适合预训练目的，使论文能够研究LLM如何解决小学数学问题。    

结果3：解答冗余度。论文检查GPT2是否通过以下方式达到高准确率：

•在生成过程中暴力计算所有参数（一种"0级"推理技能），或

•只计算给出最短解答所必需的参数（一种"1级"推理技能）。

回想一下，论文的iGSM（预训练）数据只包含必要的解答步骤（即CoT），以模拟论文在数学问题的教科书解答中看到的情况。例如，如果一个问题描述X=3+2，E=3+X，Y=X+2，并询问Y的值，那么最短的解答应该是"X=3+2=5且Y=X+2=7"，而不需要计算E。

结果3. 图4显示，GPT2主要使用"1级"推理技能解决iGSM问题，避免不必要的计算，即使在分布外评估时也是如此。

这一发现意义重大，因为它表明，与人类不同，人类通常依赖"反向推理"和草稿纸，通过从问题回溯依赖关系来写下必要的参数，而语言模型能够直接生成最短解答，无需使用草稿纸。但是，它是如何做到这一点的呢？

这个发现强调了语言模型和人类在解决数学问题时的思维过程差异。它突出了语言模型似乎具有一种直接、高效的推理能力，这种能力与人类常用的解题方法有所不同。这引发了关于语言模型内部工作机制的进一步探讨，这正是下一节要研究的内容。

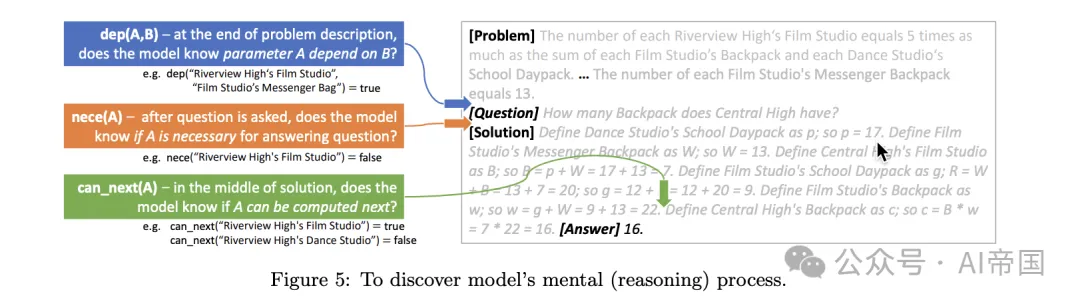
图5：揭示模型的思维（推理）过程

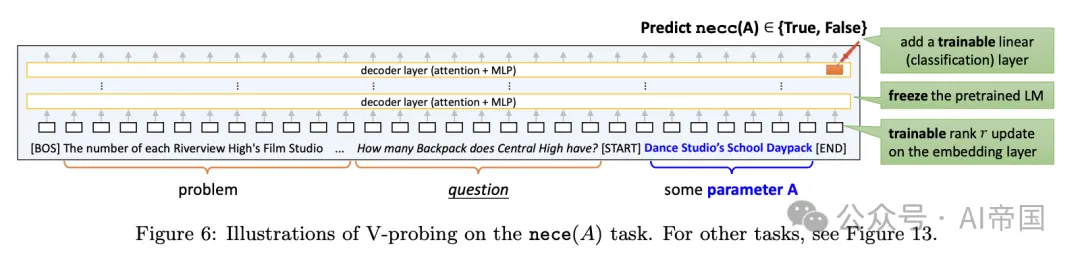
图 6：V -探查在 nece(A) 任务上的示例。其他任务见图 13。

2.4 结果 4-5：揭示模型的思维过程

为了理解模型如何学习解决数学问题，论文提出研究以下探查任务，这些任务与人类问题解决策略紧密对齐：

•nece (A)：参数 A 是否为计算答案所必需。

•dep (A, B)：在给定问题陈述下，参数 A 是否（递归地）依赖于参数 B。

•known (A)：参数A 是否已被计算。

•value (A)：参数 A 的值（介于 0-22 之间，或 23 如果 known (A)=false）。

•can_next (A)：参数A 是否可以在下一个解决方案句子中计算（即其所有前驱均已计算）。注意，A 可能并非回答问题所必需。

•nece_next (A)：参数A 是否同时满足 can_next(A) 和 nece (A)。

为了生成最短解决方案，模型必须在其思维过程中识别所有 A中 的 nece(A)。这是因为 nece (A) 是否为真直接对应于是否存在计算 A 的解决方案句子。然而，模型何时识别这一点，以及它是如何存储的？同样，它是否识别参数间的依赖关系（dep）？如果是，这一思维过程何时完成？此外，在解决方案生成过程中，模型是否始终跟踪每个参数 A 的值（value, known）？模型是否在心中知道所有可在下一句子中计算的可能参数 A（can next）？或者它只关注那些既准备就绪又必要的参数 A（nece next）？

这里提出了一种探测技术(probing technique)，以回答所有这些问题。    

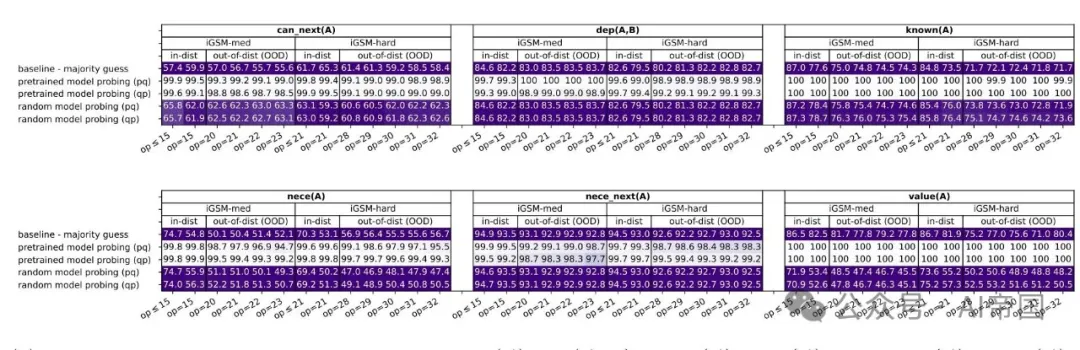
(a) 六个任务的探测准确率：can next ( A ) ，dep ( A, B ) ，known ( A ) ，nece(A)，ecenext ( A ) ，value ( A ) 。

(b) 针对正/负标签中A为不必要情况的下一个(A)、依赖(A, B)的探测准确率

图7：V-探测准确率（对于beam=1；beam=4的结果几乎相同）。详细信息见附录F.2

2.4.1 V-探测：一种近似线性探测方法

如图所示，论文在问题描述结束时对依赖任务进行探测，在必要任务的问题描述结束时进行探测。对于其他任务，论文在每个解决方案句子的末尾（包括第一个解决方案句子的开始）进行探测。

回想一下，标准线性探测涉及冻结预训练的语言模型，并检查某个属性是否在给定令牌位置的隐藏层（通常是最后一层）上线性编码。这是通过在隐藏状态上引入一个可训练的线性分类器，并对该属性执行轻量级微调任务来完成的。

论文的设置更为复杂，因为属性具有一个或两个条件变量A和B，以纯英文描述。为了处理这一点，论文将数学问题截断到探测位置，并在A（或A, B）的描述周围附加令牌[START]和[END]。然后，论文从[END]的令牌位置探测，看该属性是否在最后一层上线性编码。

与标准线性探测不同，为了考虑输入变化，论文引入了一个小的可训练的秩-8（线性）更新到输入嵌入层。论文冻结预训练的语言模型，并对所需的属性同时微调线性分类器和秩-8更新。论文将其称为V（变量）-探测。必要(A)探测任务的示意图如图6所示。    

论文计算了从iGSM预训练的语言模型的V-探测准确率，并将其与随机初始化的transformer模型的V-探测准确率进行比较。如果前者的准确率显著更高，论文可以得出结论，探测信号一定来自（或非常接近来自）预训练权重，而不是（轻量级的）微调阶段。

2.4.2 探测结果与发现

论文在图7中展示了论文的探测结果。与多数猜测和随机模型探测相比，所有任务的探测准确率都很高——除了非常困难的OOD情况（即，fo lare op，模型在这些情况下的生成准确率在图3中已经下降到S U Y_{0）。

结果4：模型像人类一样解决数学问题。论文有以下观察：

•在生成解决方案时，模型不仅记得哪些参数已经计算过，哪些还没有（值，已知），还知道接下来可以计算哪些参数（可以下一步，必要下一步）。这些能力确保模型可以像人类解决问题的技能一样，一步一步地解决给定的数学问题。

•到问题描述结束时，模型已经知道完整的必要参数列表（必要）。这表明模型已经学会了在开始生成解决方案之前，通过识别必要的参数来提前规划。这与人类行为一致，除了模型在心里计划，而人类通常会写下这些计划。这进一步证实了模型达到了第3节中讨论的“一级”推理技能。

结果 5：模型学习超越人类的推理技能。值得注意的是，模型学习器 (A, B) 和 can-next (A)，即使对于回答问题不必要的参数A，如图 7(b) 所示。这与人类解决问题的方式不同，论文通常从问题出发进行逆向推理以识别必要的参数，往往忽略了不必要的参数 [19]。相比之下，语言模型可以在问题提出之前就在头脑中预计算所有配对的依赖图 dep(A, B)。论文认为这是一种与人类行为或思维过程非常不同的“二级”推理技能。

因此，尽管这一技能对于解决数学问题并非必需，且预训练数据并未教授模型计算“全对依赖性”——仅要求计算必要的参数——模型在训练后仍能自行发现这一技能。这使得模型能够对所听到的各种关系进行排序，这一技能对于未来的任务（通过指令微调）可能非常有用。据论文所知，这可能是语言模型在预训练数据所需技能之外获得能力的首次证据；这也可能是AGI中“G”（即通用性）的初步信号（泛化到预训练数据中未教授的技能）。    

推论：逆向思维过程。AGI成功的关键问题之一是“逆向思维过程”（例如，“因为我想计算X，但X依赖于Y且Y依赖于Z，所以让我先计算Z”）是否需要在训练数据中明确包含。这与CoT不同，CoT将复杂计算分解为简单步骤，但仍需规划决定首先计算哪个步骤。

论文的发现表明，至少对于小学数学问题，在有充足数据的情况下，这一逆向思维过程可以通过语言建模自主学习，无需直接包含在训练数据中。

2.5 结果6：解释模型的错误

论文进一步探讨了探针测试结果与模型生成解决方案之间的关系，重点关注两个问题：（1）模型何时正确回答但包含了不必要的参数？(2) 是什么导致了错误的答案？论文的目标是确定模型的这种错误行为是否与模型心理过程中的错误相一致（通过探查）。

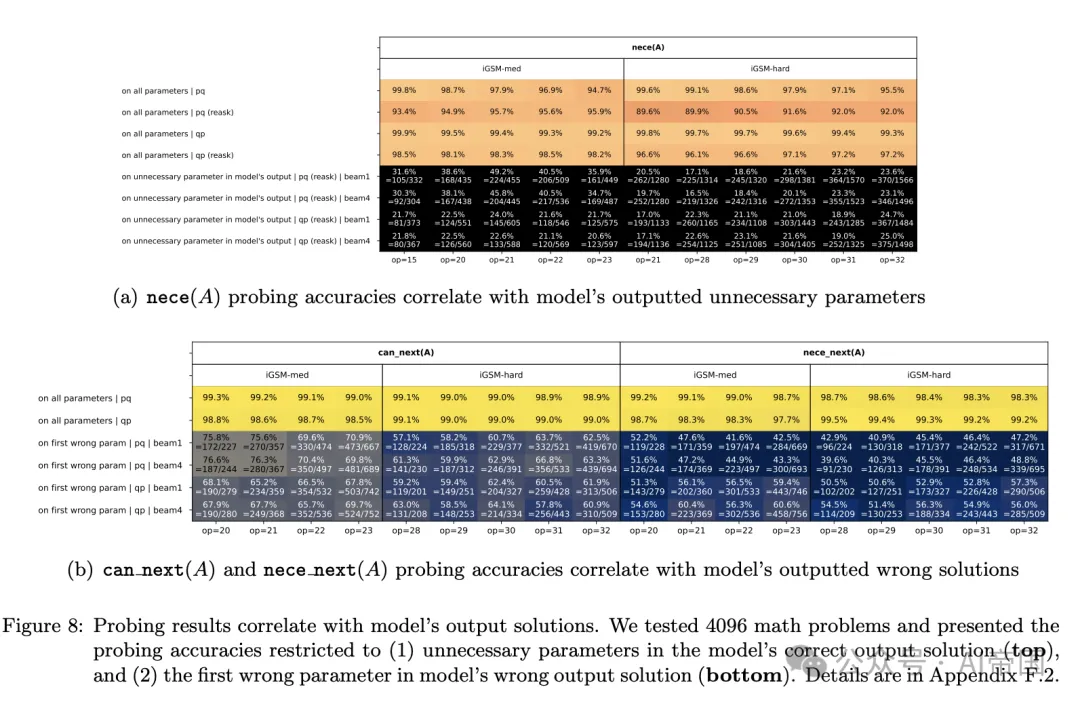
图8：探针测试结果与模型输出解决方案的相关性。论文测试了4096个数学问题，并展示了探针准确率限制在（1）模型正确输出解决方案中的不必要参数（顶部），以及（2）模型错误输出解决方案中的第一个错误参数（底部）

对于第一个问题，鉴于模型很少产生比必要步骤更长的解决方案（见图 4），论文转向了分布外的重新提问数据进行评估。17 在这类数据上，预训练模型平均每条解决方案产生约 0.5 个不必要参数，即使对于 op=32（见图 4）。论文检查了这些不必要的参数 A 是否在探查任务中被错误地预测为必要 e ( A )= 真。图 8 ( a ) 显示，这往往是事实，因此语言模型产生带有不必要步骤的解决方案，是因为它们在心理规划阶段出现了错误。    

对于第二个问题，论文关注模型的错误解决方案及其第一个错误参数。（利用合成数据，论文可以轻松识别这些参数。）论文在图 8 ( b ) 中的发现表明，模型的错误主要源于错误地预测了下一个必要 ( A ) 或下一个可能 ( A ) 为真。

结果6(图8)：基于这些结果，论文得出结论：

•语言模型所犯的许多推理错误是有系统的，根源在于其心理过程中的错误，而非仅仅是生成过程中的随机错误。

•模型在开口之前（即，在它说出第一个解决方案步骤之前），可以通过探查其内部状态发现其部分错误。

论文还观察到，GPT-4/4o 通过输出不必要参数或坚持计算参数 A 使得 can next(A) = false（参见附录 G）。这进一步暗示论文的发现可能具有更广泛的适用性。

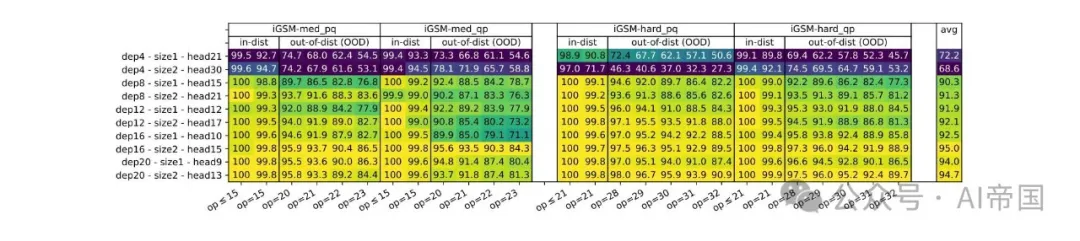
图 9：在 iGSM 数据集上预训练的不同深度/宽度的 GPT2 模型的准确率

2.6 结果 7-8：深度与推理长度

论文的控制数据集使得能够系统地探索语言模型深度与其推理长度之间的关系。

近期研究表明，对于知识存储和提取，仅模型大小至关重要（即使是 2 层transformer。此外，OpenAI 的开创性缩放定律论 和深度学习的理论研究均表明，模型深度/宽度可能在普遍范围内影响甚微。与这些发现相反，论文提出了以下观点：    

结果 7（图 9）。语言模型深度对数学推理至关重要。

接下来，论文试图揭示为何如此。论文深入研究了深度如何通过必要的探查任务影响数学问题解决能力，重点关注距离查询参数 t 处的必要参数，4/8/12/16/20。这些参数均具有必要性 (A) = true，但论文可以探查模型以观察它们在不同隐藏层预测必要性 (A) 的准确度。

图 10 展示了论文的结果。它揭示了模型层级、推理准确度与心理推理深度之间的关联。较浅层擅长预测接近查询的参数 A 的必要性 (A)，而较深层更准确，能够预测远离查询的参数的必要性 (A)。这表明模型在规划阶段采用逐层推理，递归地识别查询所依赖的所有参数，并且：

结果 8（图 10+14）。语言模型深度至关重要，可能是因为其隐藏（心理）推理过程的复杂性。对于 t 步心理推理，例如对距离查询 t 的参数 A 进行心理计算必要性 (A)，可能需要更深的模型以适应更大的 t，假设所有其他超参数保持不变。

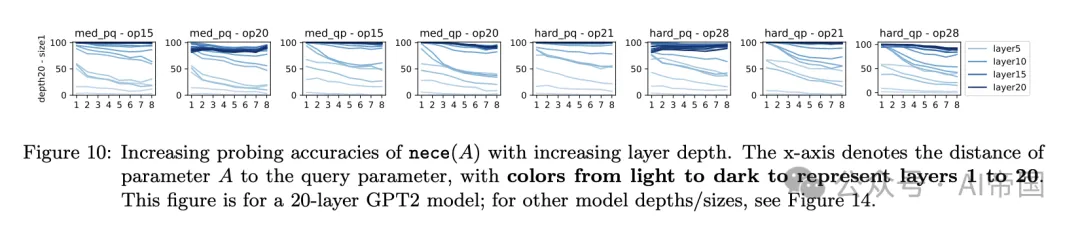
图 10：随着层深度的增加，nece(A)的探测准确性提高。x轴表示参数A与查询参数之间的距离，颜色从浅到深代表第1层到第20层。此图针对20层的GPT2模型；其他模型深度/尺寸，参见图14。

论文在此提出两点声明。首先，如果将“逆向思维过程”作为CoT添加到数据中，那么深度思维思考就不再必要，降低了语言模型对深度的要求。然而，在实践中，许多此类“思维过程”可能不会包含在标准的数学解法或一般语言中。

其次，上述说法并不意味着“t步的思维思考需要一个深度为t的transformer”。一个单一的transformer层（包含多个子层）实现t > 1的思维思考步骤是可能的，尽管随着t的增加，准确性可能会降低。论文在此文中避免提供确切的关联，因为这很大程度上取决于数据分布。

本文转载自 ​​AI帝国​​，作者： 无影寺