终于有人将机器学习中的重点做成了动画 原创

[SVM]手书动画 ✍️

除了SVM，传统机器学习中还有很多其它分类、回归和聚类算法，例如逻辑回归，决策树，随机森林等集成学习方法；这里统称为模型，这些模型基本上可以通过明确的数学公式定义输入数据与输出结果之间的关系。

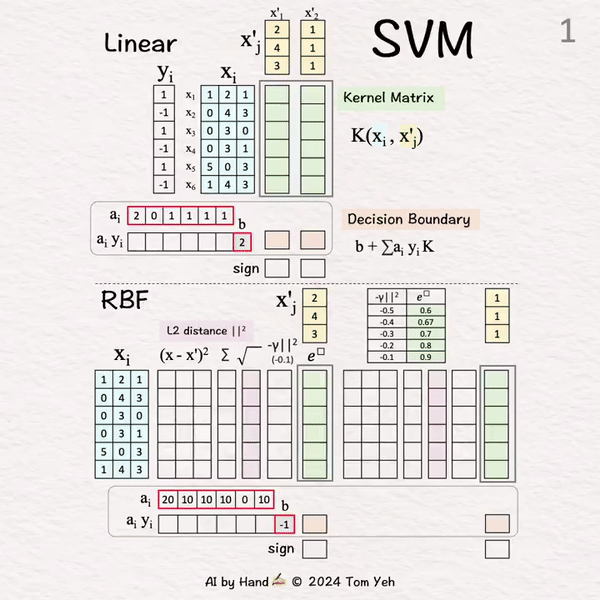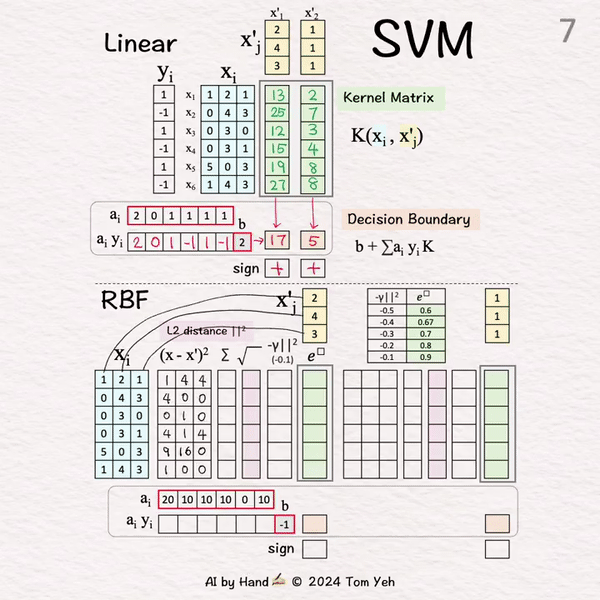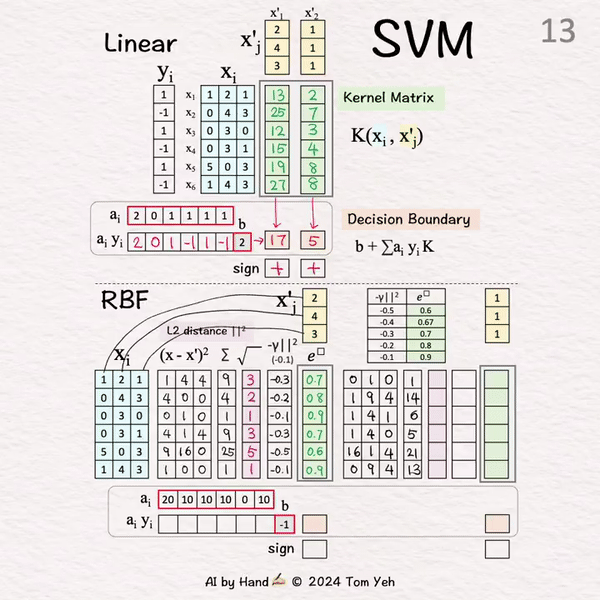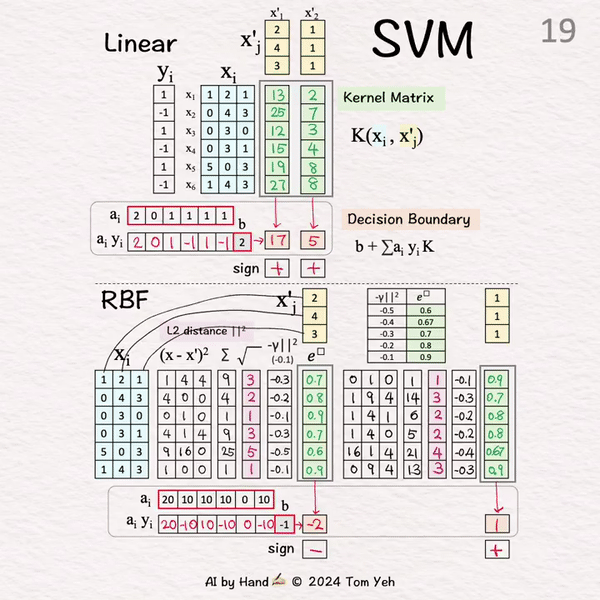
在深度学习兴起之前，支持向量机(SVM)在机器学习领域占据主导地位。

这个动画比较了线性SVM和RBF SVM。

[1] 给定:

xi: 六个训练向量(蓝色行 🟦)

yi: 标签

使用xi和yi，我们学习得到ai和b(红色边框):

ai: 每个训练向量i的系数。

，定义了决策边界

，被忽略

b: 偏置(决策边界应该移动多少)

x'j: 两个测试向量(黄色列 🟨)

(为了简化手工计算，训练和测试向量没有进行归一化。)

~ 线性SVM ~

🟩 核矩阵 (K)[2]-[3]

[2] 测试向量1

计算测试向量 🟨 与每个训练向量 🟦 的点积

点积近似两个向量之间的"余弦相似度"

输出: K的第1列

[3] 测试向量2

类似于 [2]

输出: K的第2列

🟧 决策边界 [4]-[6]

[4] 无符号系数 → 有符号权重

将每个系数与相应的标签相乘

第2个训练向量不是支持向量，因为它的系数为0。

[5] 加权组合

将权重和偏置与K相乘

输出: 到决策边界的"有符号"距离

...

X'1: (2)*13+0+(1)*12+(-1)*15+(1)*19+(-1)*27+(2) = 17

X'2: (2)*2+0+(1)*3+(-1)*4+(1)*8+(-1)*8+(2) = 5

...

[6] 分类

取符号

...

X'1: 17 > 0 →  正 +

X'2: 5 > 0 →  正 +

...

~ RBF SVM ~

给定:

ai: 学习得到的系数

b: 学习得到的偏置

🟩 核矩阵 (K)

[7]-[15]

测试向量 (X'1) 🟨 L2距离 🟪 [7]-[9]

[7] 平方差

... i=1: (1-2)^2=1,  (2-4)^2=4，(1-3)^2=4 ...

[8] 求和

[9] 平方根

[10] 负缩放

乘以-1: 注意L2是一个距离度量。取负将距离转换为相似度。

乘以gamma γ: 目的是控制每个训练样本的影响力。小的gamma意味着每个训练样本对决策边界的拉力较小，resulting in更平滑的决策边界。

结果是"负缩放的L2"

[11] 求指数

以e为底，"负缩放的L2"为指数

使用提供的表格查找e^的值

输出: K的第1列

测试向量2 (X'2) 🟨 L2距离 🟪 [12]-[14]

[12] 平方差

[13] 求和

[14] 平方根

[15] 负缩放

[16] 求指数

输出: K的第2列

🟧 决策边界 [17]-[19]

[17] 无符号系数 → 有符号权重

[18] 加权组合

...

X'1: (20)*0.7+(-10)*0.8+(10)*0.9+(-10)*0.7+0+(-10)*0.9+(-1) = -2

X'2: (20)*0.9+(-10)*0.7+(10)*0.8+(-10)*0.8+0+(-10)*0.9+(-1) = 1

...

[19] 分类

...

X'1: -2 < 0 →  -

X'2: 1 > 0 →  +

...

[反向传播] 手书动画✍️

有了模型，接下就需要通过优化算法求模型中的参数，也就是数学公式中的未知量。

[1] 前向传播

↳ 给定一个三层的多层感知器，输入向量为X，预测结果为Y^{Pred} = [0.5, 0.5, 0]，真实标签为Y^{Target} = [0, 1, 0]。

[2] 反向传播

↳ 添加单元格以存放我们的计算结果(梯度信息)。

[3] 第三层 - Softmax（蓝色）

↳ 使用化简后的公式直接计算 ∂L / ∂z3：Y^{Pred} - Y^{Target} = [0.5, -0.5, 0]。

↳ 这个化简后的公式得益于Softmax和交叉熵损失的联合使用。

[4] 第三层 - 权重（橙色）和偏置（黑色）

↳ 通过将 ∂L / ∂z3 和 [ a2 | 1 ] 相乘，计算 ∂L / ∂W3 和 ∂L / ∂b3。

[5] 第二层 - 激活（绿色）

↳ 通过将 ∂L / ∂z3 和 W3 相乘，计算 ∂L / ∂a2。

[6] 第二层 - ReLU（蓝色）

↳ 通过将 ∂L / ∂a2 乘以1（对正值）或0（对负值），计算 ∂L / ∂z2。

[7] 第二层 - 权重（橙色）和偏置（黑色）

↳ 通过将 ∂L / ∂z2 和 [ a1 | 1 ] 相乘，计算 ∂L / ∂W2 和 ∂L / ∂b2。

[8] 第一层 - 激活（绿色）

↳ 通过将 ∂L / ∂z2 和 W2 相乘，计算 ∂L / ∂a1。

[9] 第一层 - ReLU（蓝色）

↳ 通过将 ∂L / ∂a1 乘以1（对正值）或0（对负值），计算 ∂L / ∂z1。

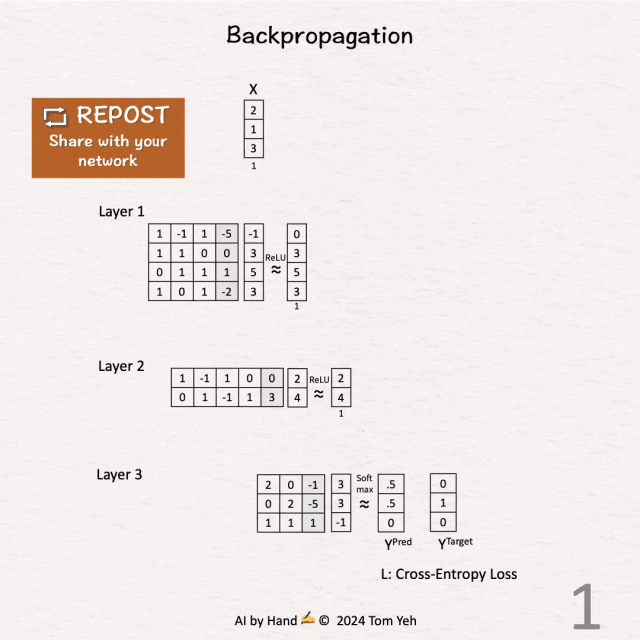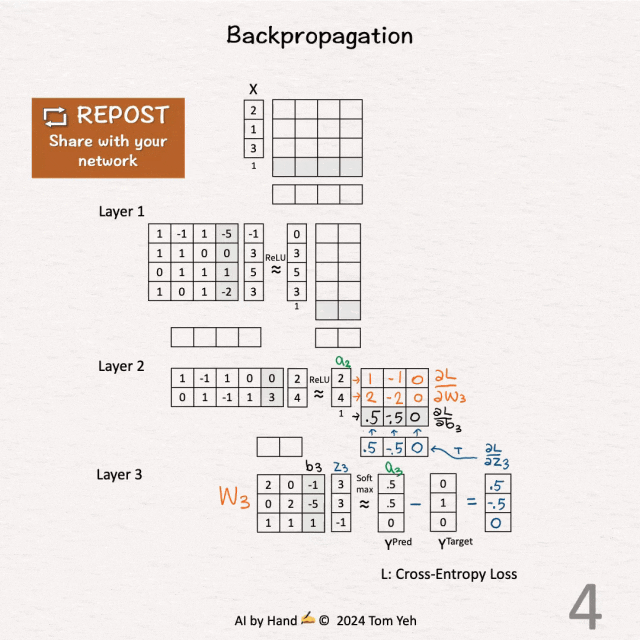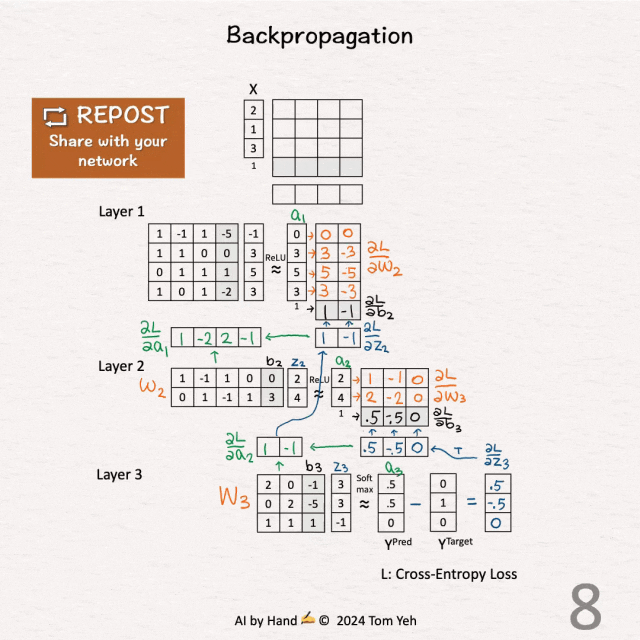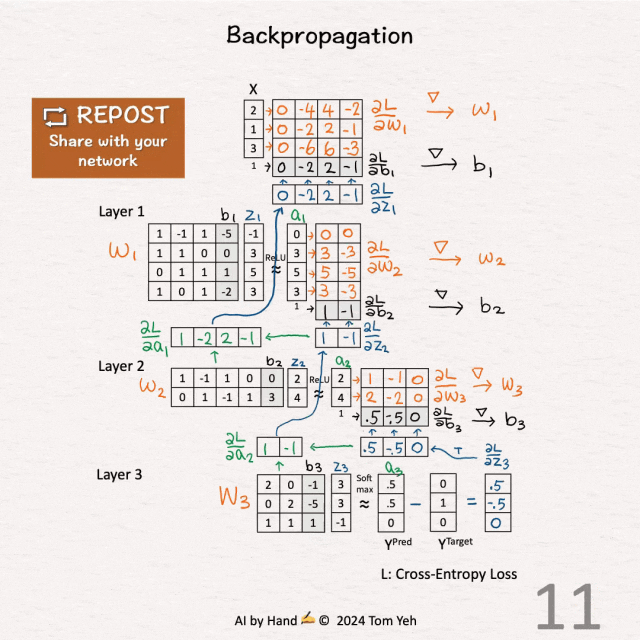
[10] 第一层 - 权重（橙色）和偏置（黑色）

↳ 通过将 ∂L / ∂z1 和 [ x | 1 ] 相乘，计算 ∂L / ∂W1 和 ∂L / ∂b1。

[11] 梯度下降

↳ 更新权重和偏置（通常在这里应用学习率）。

💡 矩阵乘法是关键：正如在前向传播中一样，反向传播也主要是矩阵乘法。你完全可以像我在这个练习中演示的那样手动计算，尽管速度慢且不太完美。这就是为什么GPU高效矩阵乘法能力在深度学习中扮演重要角色的原因，这也是为什么NVIDIA的估值现在接近1万亿美元的原因。

💡 梯度爆炸：我们可以看到即使在这个简单的三层网络中，随着反向传播的进行，梯度正在变大。这促使我们使用诸如ResNet中跳跃连接（skip connections）的方法来处理梯度爆炸（或消失）问题。

[Multiple Layer Perceptron（MLP）]手书动画✍️

MLP更准确地说应该属于神经网络范畴，作为一种分类、回归模型，在很多地方都能看到它的身影，例如，目标检测，Transformer等。

通过隐藏层和激活函数的使用，它能够模拟任意复杂函数，与传统机器学习相比，它大大减小对经验的依赖。

步骤说明

给定一个代码模板（左侧），实现如图所示的多层感知器（右侧）。

第一个线性层。

输入特征大小为3。输出特征大小为4。我们可以看到权重矩阵的大小是4×3。此外，还有一个额外的列用于偏置（bias = T）。激活函数是ReLU。我们可以看到ReLU对第一个特征的影响（-1 -> 0）。

第二个线性层。

输入特征大小为4，与前一层的输出特征大小相同。输出特征大小为2。我们可以看到权重矩阵的大小是2×4。但是，没有额外的列用于偏置（bias = F）。激活函数是ReLU。

最后的线性层。

输入特征大小为2，与前一层的输出特征大小相同。输出特征大小为5。我们可以看到权重矩阵的大小是5×2。此外，有一个额外的列用于偏置（bias = T）。激活函数是Sigmoid。我们可以看到Sigmoid的效果，它是一个将原始分数（3, 0, -2, 5, -5）非线性映射到0到1之间的概率值的函数。

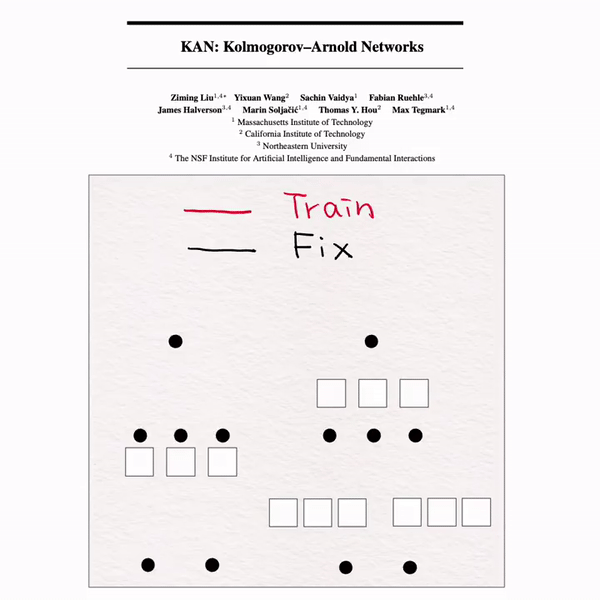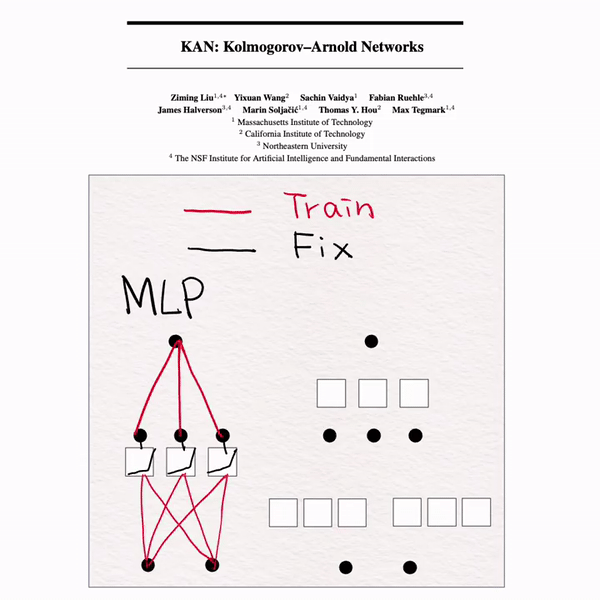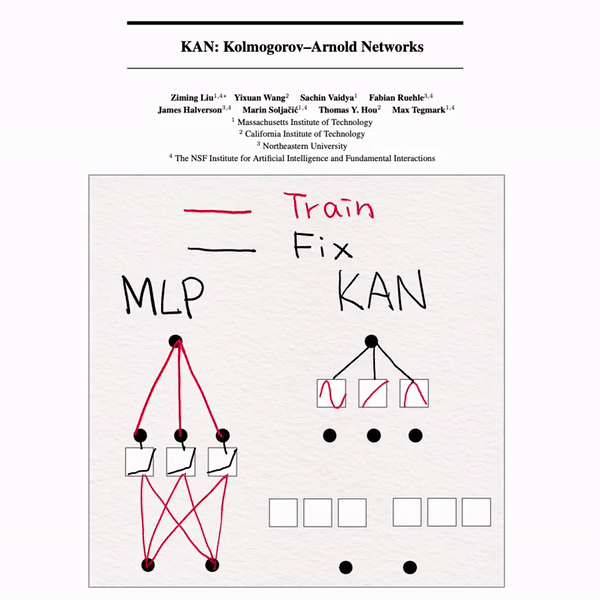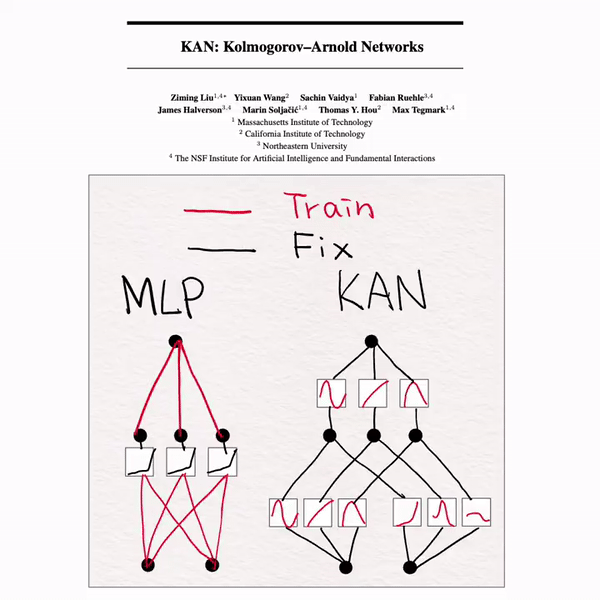
[MLP vs KAN]手书动画✍️

Transformer中MLP占据了很大一部分参数，为了提升Transformer计算效率，有人提出了KAN和MoE来作为MLP的一种替代。

本文转载自公众号人工智能大讲堂 

原文链接：​​https://mp.weixin.qq.com/s/x-mlK_S_HIRquAxr8uNVXQ​​