三个臭皮匠与一个诸葛亮：覆盖率与正确率的博弈

将语言模型不断地扩大规模是可以提高它们的能力。而日常运用的时候，通常将推理限制在一次。要是对于同一个问题进行多次反复的采样生成，那么是否能够覆盖正确的答案？是否能够被准确的捞出？

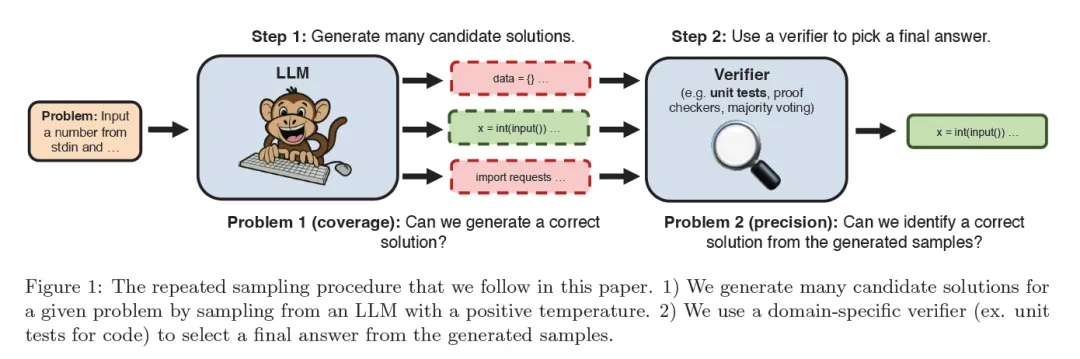
最近一项研究进行如下的探索。整个过程如上图所示，它分为两个步骤，准备一个问题，然后遵循重复采样程序，通过具有正温度（代表着回答多样性）的LLM中采样来为给定问题生成很多的K个候选解决方案。第二个步骤使用特定领域的验证器从生成的样本中选择最终答案。

<简单总结一下：可以多次生成，但是成本要低且要包含正确答案。在解决了第一个问题之后，还要解决从K个答案，例如10000个中挑出那个正确的。>

1.覆盖率能上去

覆盖率的定义为被解决问题的比例，被解决的问题至少要在K个答案中被解开一次。这项研究对SWE-bench Lite这个基准进行重复采样回答，使用DeepSeek-V2-Coder-Instruct来解决问题具有15.9%的正确率，若仅仅生成一次的回答（样本）。若让其生成250次的回答，则覆盖率飙升至56%。这个成绩也远远强于前沿模型的单次回答43%正确率。

细心的读者会提出抗议，会不会比较费钱。其实按照当前的API定价，即便用调用5次的DeepSeek模型，也比GPT-4o或Claude 3.5 Sonnet的单次回答性价比更高且能够解决更多的问题。<下面就是价格的对比图！>

研究中发现，覆盖率和样本数量之间的关系通常是对数线性的，可以用指数幂律来建模，这表明存在推理时间缩放定律。

在解决 GSM8K和MATH的数学单词问题时，Llama-3模型在10000次的样本中对于正确答案的覆盖率增长到95%以上。 从样本集合中选择正确解决方案的常用方法（例如多数投票或奖励模型）在超过数百个样本时会趋于稳定。

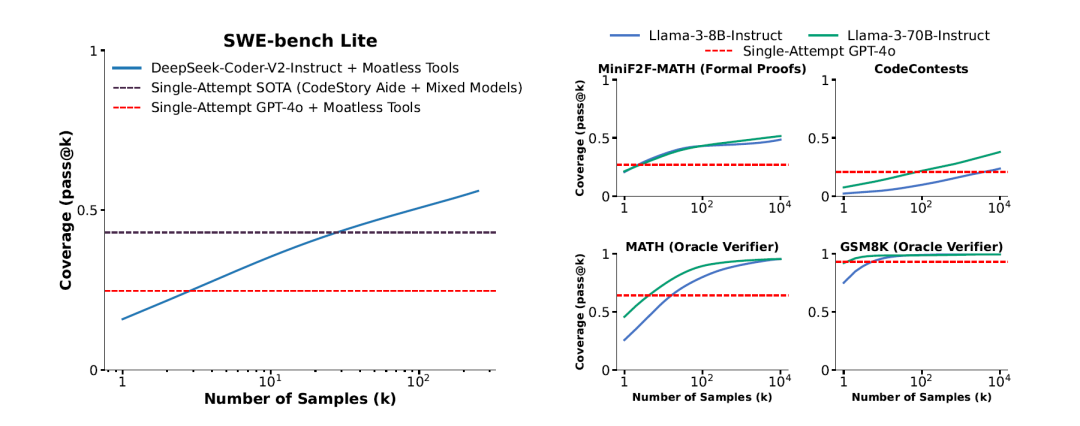
在五项任务中，值得注意的是，使用重复采样，能够将SWE-bench Lite上的解决率从15.9%提高到56%。

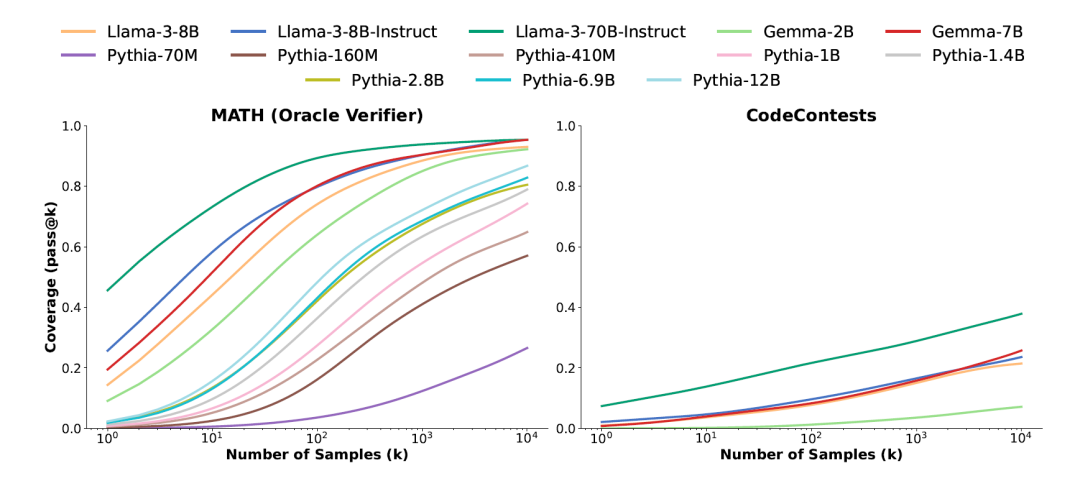
本次的研究将评估限制在MATH和CodeContests数据集上，以最大限度地降低推理成本，测试中几乎每个模型的覆盖率都有所增加，当应用重复采样时，较小的模型显示出最明显的覆盖率增加。

在CodeContests上，Gemma-2B的覆盖率增加了300多倍，从pass@1<1代表1次抽样>的0.02%增加到pass@10k<10k代表10000次抽样>的7.1%。使用Pythia-160M解决MATH问题时，覆盖率从pass@1 的0.27%增加到pass@10k的57%。

这种跨模型覆盖率增加模式的例外是在 CodeContests 上评估的 Pythia 系列则为例外，所有Pythia模型在这个数据集上的覆盖率都为零，即便10,000个样本也是如此。推测可能是因为Pythia接受的特定的编码数据比 Llama和Gemma少。

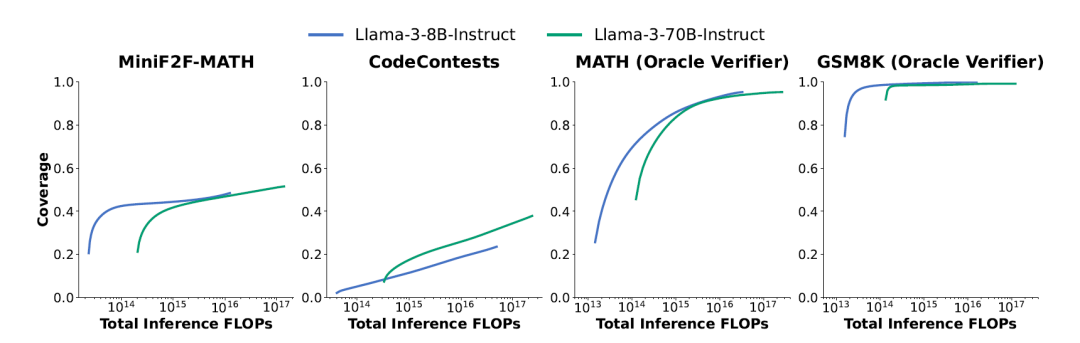
重复采样可以放大较弱模型的功能，并超越来自较强模型的单个样本。在这里还是需要证明这种放大比使用大规模的参数模型更具成本效益。上图将之前抽样次数的成本采用FLOP（视为成本指标）重新绘制了统计图。

在MiniF2F、GSM8K和MATH的评估指标上，当FLOP预算固定时，Llama-3-8B-Instruct总是比更大（且更昂贵）的70B模型获得更高的覆盖率。然而对于 CodeContests，70B模型几乎总是更具成本效益！！

每次查询折算的FLOP公式如下：

LLM的Loss与其训练计算算力之间的关系已通过​​缩放定律<链接温习！>​​讲解得很是清晰。这些定律在经验上已经被验证，并激发了模型开发人员的信心，相信只要投资大量的算力则能够得到很棒的模型。

受到训练缩放定律的启发，旨在更好地描述覆盖率和样本预算（即多次推理的计算量）之间的关系，这里观测到两个很有意思的想象：

• 覆盖率和样本数量之间的关系通常可以用指数幂律建模。

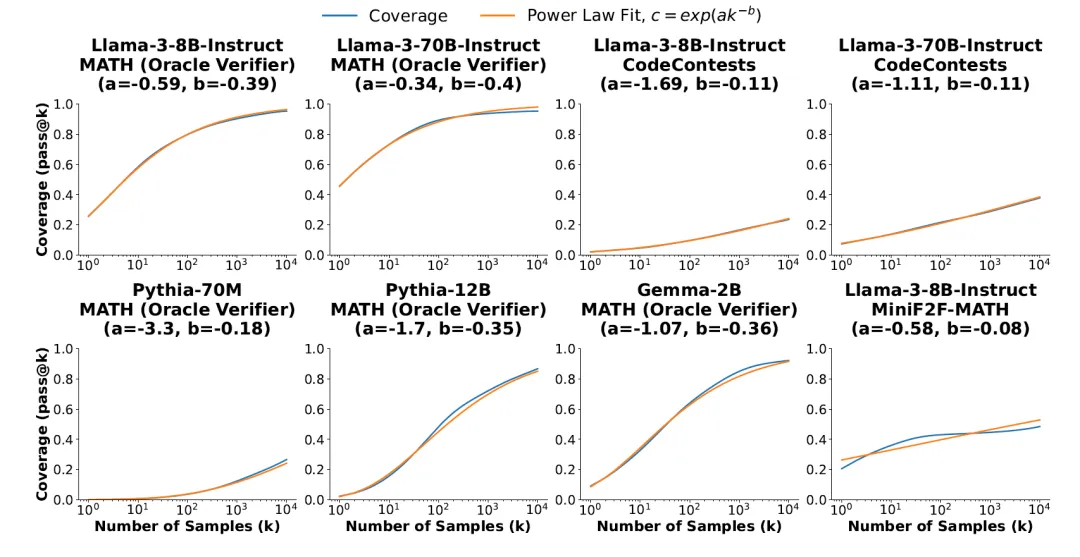
• 对于给定的任务，来自同一家族的不同模型的覆盖率曲线类似于具有相似斜率但不同水平偏移的 S 曲线

  

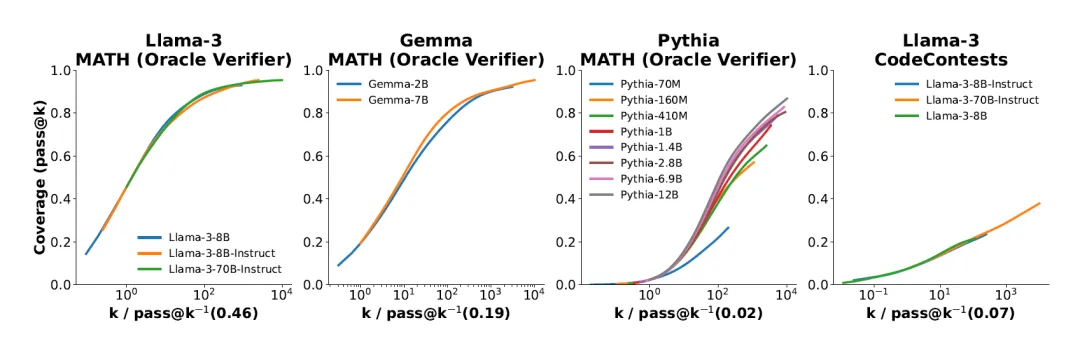
2.如何选择对的

覆盖率上去了，那么如何万里挑一呢？研究发现在没有自动验证器的领域中，从许多代中识别出正确的样本仍然是未来研究的重要方向。

既然已经存在N个回答，如何挑选一个最为最后的答案，就像人生如何选择一样至关重要。第2阶段关注的重点在于多次采样中如何选择出最佳答案，以便提高正确率。目前存在主流的三种方法：多数投票（Majority Voting），奖励模型选择（Reward Model Selection），奖励模型多数投票（Reward Model Majority Voting）。

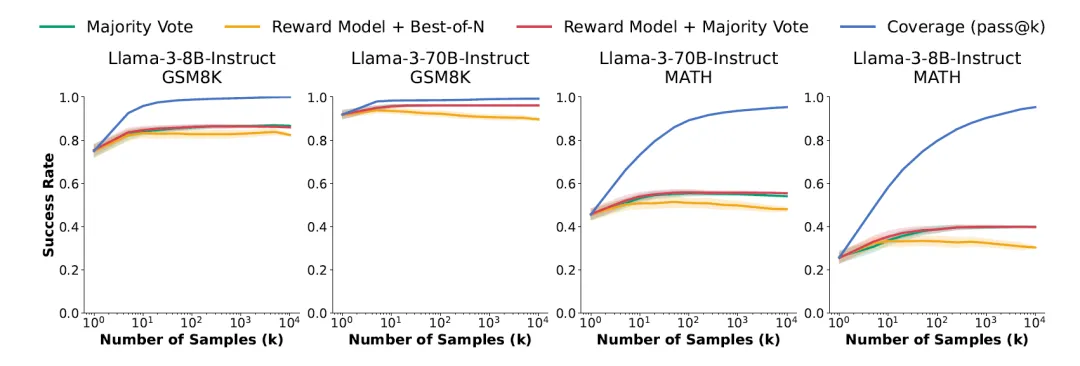
研究表明，随着样本数量的增加，前面三种组合式的选择会随着样本数量的增加而增加，但在100个样本左右达到饱和。而覆盖率(图4）会随着样本数量的增加而继续增加，并超过95%。

<！！注意，覆盖率意味着这么多的备选答案存在正确的，但是并不代表算法可以检索出正确作为最后的答案！！>

在多数投票的情况下，这种成功率饱和很容易解释。随着样本数量的增加，分配给每个答案的投票比例会稳定下来，因此成功率也会稳定下来。对于某些GSM8K和MATH问题，正确解决方案的采样概率为1%或更低，因此它们只是少数样本。随着样本数量的增加，更多问题会出现罕见的正确解决方案，从而增加覆盖率，但不会提高多数投票的成功率。

为了充分利用重复采样的优势，识别出正确解答一定要能够解决这些“大海捞针”的场景，识别出稀有的正确样本。在数学应用题中，现有工具无法自动验证答案，研究者发现覆盖率与确定最终答案的方法选择存在很大差距。

<即便抽样了N次，还是要选择一个不是？！>。

当使用Llama-3-8B-Instruct解决数学问题时，覆盖率从100个样本的79.8%增加到10,000个样本的95.3%。然而，多数投票和使用奖励模型来选择最终解答的方法在样本预算较低的情况下趋于饱和，在同一范围内仅从38.7%扩展到39.8%。

<即便有了正确答案，还是选不中！？>。

这些结果表明构建强大的验证器仍然是一个悬而未决的问题。

本文转载自​​鲁班模锤​​，作者： 庞德公 ​​​​