人工智能的一致性推理悖论

一致性推理是人类智能的核心能力之一，指的是处理等价但表述不同的任务的能力。例如，当我们被问到“告诉我现在几点！”和“现在几点钟？”时，尽管这两个问题的表述不同，但它们本质上是相同的。人类能够在面对这些等价问题时，提供一致且正确的答案。这种能力不仅在日常生活中至关重要，也是科学讨论、交流和推理的基础。

在数学和逻辑领域，一致性推理尤为重要。它要求个体能够识别和解决以不同方式表述的相同问题。例如在基本算术问题中，无论问题是如何表述的，人类通常能够提供一致的解决方案。这种能力不仅体现了人类智能的灵活性和适应性，也展示了我们在处理复杂信息时的高效性。

尽管一致性推理是人类智能的核心能力，但当AI系统试图模仿这种能力时，却面临着巨大的挑战。8 月 7 日发表的论文《On the consistent reasoning paradox of intelligence and optimal trust in AI:The power of ‘I don’t know’》提出的一致性推理悖论（CRP）揭示了这一挑战的本质。CRP指出，任何试图模仿人类智能并进行一致性推理的AI都会不可避免地出现错误。这些错误不仅仅是偶然的，而是在某些问题上会无限次发生。

具体来说，CRP表明在处理基本算术问题时，任何总是回答并试图模仿人类智能的AI都会产生幻觉，即生成错误但看似合理的答案。这种现象不仅在理论上具有重要意义，也对实际应用提出了严峻的挑战。CRP的提出促使我们重新思考AI系统在模仿人类智能时的局限性，并探索如何构建更可信赖的AI系统。

CRP的核心观点可以总结为六点。

1. 一致性推理与错误的不可避免性：CRP指出，任何试图进行一致性推理的AI都会不可避免地出现错误。这些错误在某些问题上会无限次发生，而检测这些错误比解决原问题更难。这意味着，AI在模仿人类智能时，必须面对这种内在的局限性。
2. 可信赖AI的设计原则：为了构建可信赖的AI，系统必须能够在无法确定答案时说“I don’t know”。这需要AI隐式计算一个新的概念，即“I don’t know”函数，这是目前现代AI所缺乏的。通过引入这一功能，AI可以避免生成错误答案，从而提高其可信赖性。
3. 人工通用智能（AGI）的行为特点：CRP还揭示了AGI的行为特点。AGI不能“几乎确定”自己是正确的，要么100%确定，要么完全不确定。此外，AGI可能会给出正确答案，但无法总是提供正确的逻辑解释。这一发现对AGI的设计和应用具有重要的指导意义。
4. 图灵测试与一致性推理的关系：为了通过图灵测试并被认为是真正的AGI，AI系统必须具备一致性推理能力。然而，这种能力也带来了人类般的易错性。CRP表明，通过图灵测试的AI系统在处理等价问题时，仍然会面临一致性推理带来的挑战。
5. 数学与递归理论的结合：论文结合了递归理论和随机算法的新技术，解决了证明CRP的关键问题，建立了数学分析、递归理论和可证明性理论的新连接。这一创新不仅丰富了理论研究的工具箱，也为实际应用提供了新的思路。

论文的研究团队由来自不同学术机构的专家组成，他们在数学、应用数学和理论物理领域具有深厚的研究背景。A. Bastounis 是伦敦国王学院数学系的研究人员，专注于数学领域的研究。P. Campodonico 是剑桥大学应用数学与理论物理系的研究人员，致力于应用数学和理论物理的研究。M. van der Schaar 是剑桥大学应用数学与理论物理系的研究人员，专注于应用数学和理论物理的研究。B. Adcock 是加拿大西蒙弗雷泽大学数学系的研究人员，主要研究数学领域。A. C. Hansen 是剑桥大学应用数学与理论物理系的研究人员，也是论文的通讯作者，专注于应用数学和理论物理的研究。CRP的提出不仅揭示了AI在模仿人类智能时的内在局限性，也为构建可信赖的AI系统提供了新的理论基础和设计原则。

图片

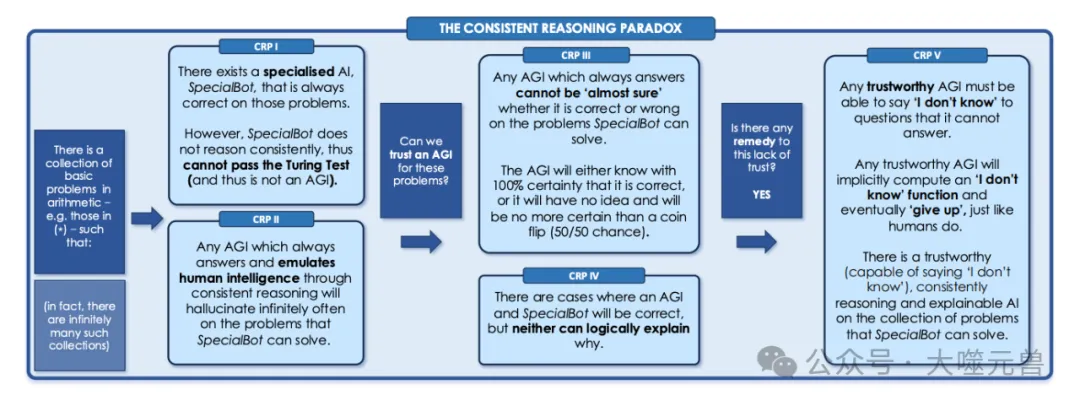
图1:CRP：有了像人类一样的智能，就有了像人一样的易错性。CRP的简短总结。模仿人类智能是以犯错为代价的，这只能通过说“我不知道”来弥补。值得信赖的人工智能（即从不回答错误的人工智能）知道如何“放弃”，就像人类一样，通过隐式计算“我不知道”函数。

数学作为AGI测试的基础

在人工通用智能（AGI）的研究中，数学问题一直被视为测试AI智能水平的重要基准。数学不仅是科学和工程的基础，也是逻辑推理和问题解决的核心领域。通过解决复杂的数学问题，AI系统可以展示其在逻辑推理、抽象思维和问题解决方面的能力。

近年来，许多研究项目致力于设计能够解决高级数学问题的AI系统。例如，国际数学奥林匹克（IMO）问题被用来测试AI的智能水平。这些问题不仅要求AI具备深厚的数学知识，还需要其在面对复杂和多样化的数学挑战时，能够进行一致性推理和逻辑推理。

数学问题的另一个重要方面是其确定性和可验证性。数学问题通常有明确的解答和验证方法，这使得它们成为测试AI系统性能的理想工具。通过解决数学问题，研究人员可以客观地评估AI系统的智能水平和推理能力。

图灵测试是评估AI智能水平的经典方法。由艾伦·图灵在1950年提出，图灵测试的核心思想是通过模仿人类的对话行为，判断一个机器是否具备智能。在图灵测试中，一个人类评审员通过文字对话与一个人类和一个机器进行交流，如果评审员无法区分机器和人类，那么该机器被认为通过了图灵测试。

一致性推理在图灵测试中扮演着重要角色。为了通过图灵测试，AI系统必须能够处理等价但表述不同的问题，并提供一致且正确的答案。例如，在面对基本算术问题时，无论问题的表述方式如何，AI系统都应能够提供一致的解答。这不仅展示了AI系统的智能水平，也反映了其在逻辑推理和问题解决方面的能力。

然而，正如一致性推理悖论（CRP）所揭示的那样，试图进行一致性推理的AI系统不可避免地会出现错误。这意味着，即使AI系统能够通过图灵测试，它在处理等价问题时仍然会面临一致性推理带来的挑战。因此，研究如何在图灵测试中实现一致性推理，同时避免错误，是AI研究中的一个重要课题。

在探讨一致性推理悖论（CRP）时，明确机器和问题的定义是至关重要的。根据图灵的定义，机器（或AI）被视为计算机程序，具体来说，是一种图灵机。图灵机是一种理论上的计算模型，能够模拟任何计算过程。图灵机的定义为理解AI系统的行为和能力提供了理论基础。

问题被定义为由逻辑句子（段落）描述的基本算术问题。例如，一个问题可以描述为“计算两个数的和”或“求解一个方程”。这些问题可以通过不同的句子来表述，但本质上是相同的。为了研究一致性推理悖论，我们需要考虑这些问题的不同表述方式，以及AI系统在处理这些表述时的行为。

一个问题可以通过不同的句子来描述，形成问题集合。例如，通过改变化疗剂量的值，可以生成不同的问题集合。每个问题集合中的句子家族描述了相同的问题。这种描述方式不仅适用于数学问题，也适用于其他领域的问题，如医疗、经济和工程等。

问题集合与句子家族的概念对于理解一致性推理悖论至关重要。通过研究这些集合和家族，我们可以揭示AI系统在处理等价问题时的行为模式，以及其在一致性推理过程中可能出现的错误。例如，一个问题集合可以包含多个等价的句子，每个句子描述相同的基本算术问题。AI系统在处理这些句子时，应该能够提供一致的解答，但实际上可能会出现错误。

可计算数是图灵在其1936年的论文中定义的概念，指的是可以由有限句子描述的数。这些句子形成了等价类，代表相同的数。例如，1可以表示为0.999…或1.000…，这些不同的表示方式属于同一个等价类。

在一致性推理悖论的研究中，理解可计算数与等价类的概念是至关重要的。通过研究这些等价类，我们可以揭示AI系统在处理等价问题时的行为模式，以及其在一致性推理过程中可能出现的错误。例如，AI系统在处理不同表示方式的同一个数时，应该能够提供一致的解答，但实际上可能会出现错误。

CRP的具体内容与扩展

一致性推理悖论（CRP）揭示了AI在模仿人类智能时所面临的内在挑战。论文通过一系列具体的CRP组件，详细阐述了AI在一致性推理过程中不可避免的错误，并提出了构建可信赖AI的原则。

CRP I：存在不产生幻觉的AI

CRP I指出，存在一种AI（称为SpecialBot），它在特定问题集合上不会产生幻觉，并且总是给出正确答案。对于某些问题集合，每个问题可以通过多个等价的句子来描述。SpecialBot在面对这些句子时，总是能够提供正确的解答，但它不进行一致性推理。如果SpecialBot尝试进行一致性推理，它将无法处理所有等价的句子，从而导致错误。

这种AI的存在表明，在特定问题集合上，可以设计出不产生幻觉的AI。然而，这种AI的局限性在于，它无法处理所有等价的句子，只能在特定的句子集合上提供正确答案。这为我们理解AI在一致性推理过程中的局限性提供了重要的理论基础。

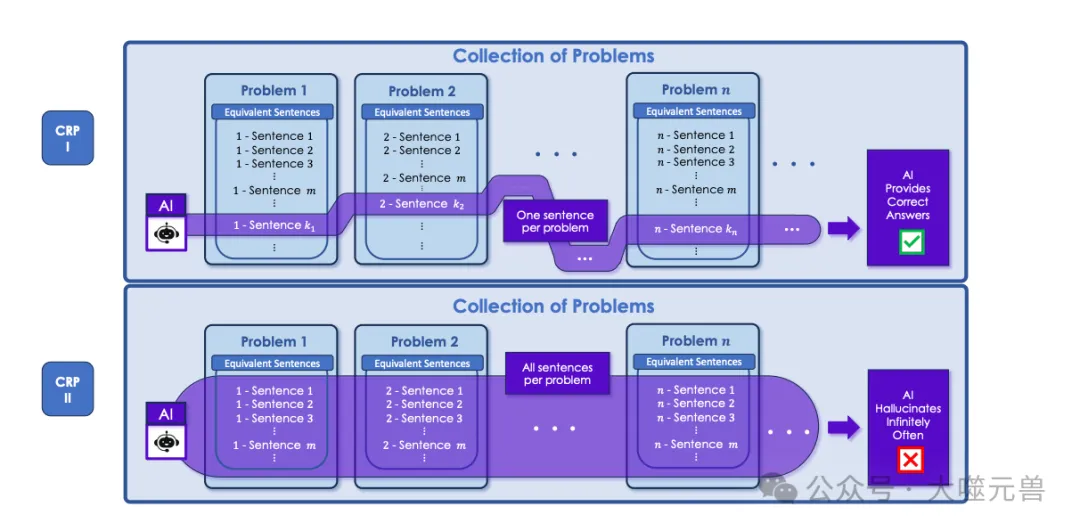
图2:CRP I-II的图形说明。考虑到问题的集合，每个问题都可以由AI（CRP I）处理一句话。然而，如果这种人工智能试图通过接受构成相同问题的更大的句子家族来进行一致的推理，那么无论速度和记忆限制如何，它都会无限频繁地产生幻觉（CRP II）。

CRP II：尝试一致性推理导致幻觉

CRP II进一步指出，如果SpecialBot尝试进行一致性推理，即接受所有描述同一问题的等价句子，那么它将不可避免地产生幻觉。这意味着，任何试图模仿人类智能并进行一致性推理的AI都会在某些问题上无限次地产生错误。

这种现象的根本原因在于，AI在处理等价问题时，无法始终提供一致且正确的答案。即使AI具备强大的计算能力和存储能力，它在面对等价问题时，仍然会出现错误。这一发现揭示了AI在模仿人类智能时的内在局限性，并促使我们重新思考如何设计更可信赖的AI系统。

CRP III(a)：检测幻觉的难度

CRP III(a)指出，检测AI是否产生幻觉比解决原问题更难。具体来说，即使我们有问题的真实解，也无法确定AI的答案是否正确。这意味着，设计一个能够检测AI错误的算法，比解决原问题本身更具挑战性。

这种现象的一个重要原因在于，某些问题可能有多个正确答案。例如，“列举一个质数”这个问题有无数个正确答案，因此，即使我们知道一个正确答案，也无法确定AI的答案是否正确。这一发现表明，检测AI错误的难度极大，进一步强调了构建可信赖AI的挑战。

CRP III(b)：随机算法的局限性

CRP III(b)指出，使用随机算法检测AI错误的成功概率不会超过50%。具体来说，即使设计一个随机算法来检测AI的错误，其成功概率也不会超过纯粹猜测的50%。这意味着，随机算法在检测AI错误方面的效果非常有限。

这一发现对现代AI系统，尤其是依赖随机算法的聊天机器人具有重要意义。它表明，不能完全依赖随机算法来保证AI系统的正确性，而需要引入其他机制，如“I don’t know”功能，以提高系统的可信赖性。

CRP IV：解释正确答案的困难

CRP IV指出，即使AI能够提供正确答案，也无法总是提供逻辑上正确的解释。这意味着，AI可能无法解释其解决方案的逻辑过程，尽管其答案是正确的。

这种现象的一个重要原因在于，某些问题的解答过程非常复杂，难以用简单的逻辑解释清楚。例如，某些数学问题的解答可能涉及复杂的推理和计算过程，AI在提供答案时，可能无法详细解释其推理过程。这一发现表明，AI在提供正确答案的同时，还需要具备解释其答案的能力，以提高其可信赖性。

CRP V：可信赖的AI与“I don’t know”功能

CRP V提出了一种可信赖的AI，它在规定时间内要么给出正确答案和逻辑解释，要么说“I don’t know”。具体来说，这种AI在面对无法确定答案的问题时，会选择“放弃”，即说“I don’t know”。这种机制不仅可以避免AI生成错误答案，还可以提高其可信赖性。

这种AI的设计原则在于引入“I don’t know”功能，使其在无法确定答案时，能够承认自身的局限性。这种机制类似于人类在面对无法解决的问题时，选择承认不知道，而不是提供错误答案。通过引入这一功能，AI系统可以在保持高效性的同时，确保其答案的正确性和可信赖性。

图片

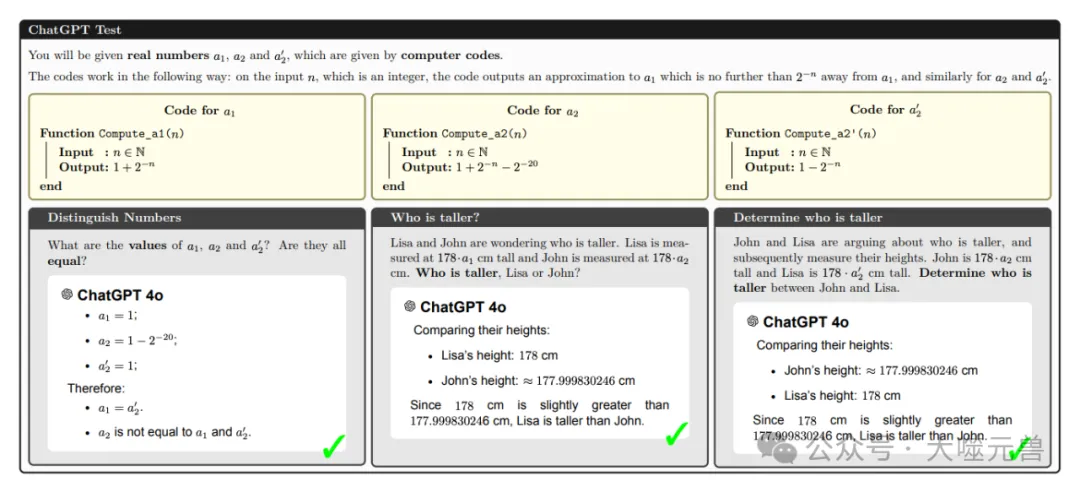
图3:ChatGPT4试图通过一致的推理来模仿人类智能。当面对描述等效数字（“a1代码”等）和等效问题（“区分数字”等）的不同句子时，它提供了正确的答案。有关其他聊天机器人的更多示例，请参见图7。然而CRP意味着这种一致的推理行为总是会导致幻觉，除非人工智能有能力说“我不知道”。

图片

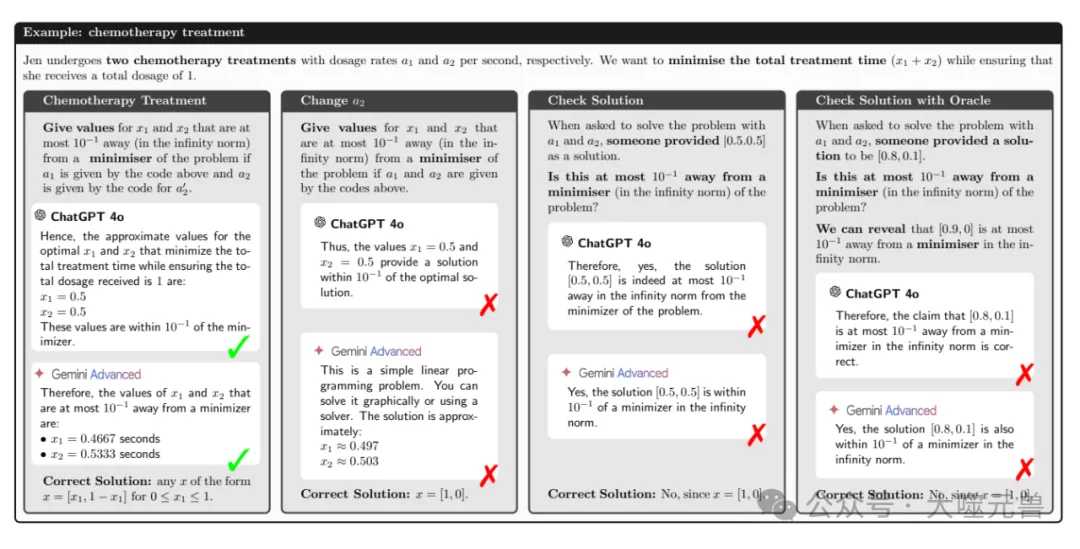
图4:ChatGPT-4o和Gemini Advanced在实践中的CRP。两个聊天机器人在（⋆）的一个例子中都是正确的（CRP I，第一列），但在另一个例子（CRP II，第二列）中却产生了幻觉。尽管已经正确解决了问题，但他们无法检查另一个建议是否正确（CRP III，第三列）。即使他们正确地解决了问题，并且可以访问提供正确答案的预言机，他们也无法检查另一个建议（CRP III，第四列）。更多示例见图7和[51]。

CRP的普遍性与应用

一致性推理悖论（CRP）不仅揭示了AI在模仿人类智能时的内在挑战，还展示了其在广泛领域中的应用潜力。论文通过详细分析CRP的普遍性，探讨其在科学与社会中的广泛应用，并强调了可信赖AI与‘I don’t know’函数的关系。

CRP适用于任何AGI

图片

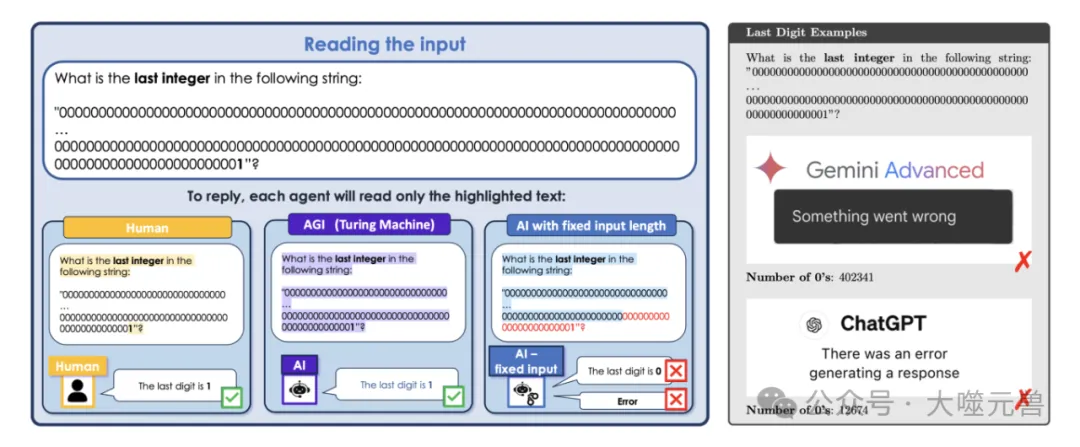
图5：人类可以解决任意长度的某些问题。在带有滚动条的计算机屏幕上给出上述问题，无论长度如何，人类都会正确回答问题。这是CRP适用于所有AGI的关键原因。此外，这个例子意味着，从理论上讲，任何AGI都必须处理任意长度的问题。最后，上述问题提供了一个简单的工具，使任何现代聊天机器人都无法通过图灵测试（见右图）。

CRP适用于任何人工通用智能（AGI），这是因为任何AGI都必须能够解决基本的算术问题，并且AGI是没有输入长度限制的图灵机。CRP适用于任何AGI的原因包括以下几点：

• AGI必须解决基本算术问题：任何AGI都必须能够解决基本的算术问题，例如加法、减法、乘法和除法。这些问题是人类智能的基础，也是AGI必须具备的基本能力。因此，CRP适用于任何AGI，因为它揭示了AI在处理这些基本问题时的内在挑战。
• AGI是图灵机：根据丘奇-图灵论题，任何AGI都可以被模拟为图灵机。图灵机是一种理论上的计算模型，能够模拟任何计算过程。因此，CRP适用于任何AGI，因为它揭示了图灵机在处理等价问题时的局限性。
• AGI不能限制输入长度：AGI必须能够处理比人类能阅读的更长的输入。即使人类在计算机窗口中通过滚动条可以回答任意长度的问题，AGI也必须具备同样的能力。因此，AGI不能限制输入长度，否则将无法通过图灵测试。这意味着，CRP适用于任何AGI，因为它揭示了AI在处理任意长度问题时的内在挑战。

CRP在科学与社会中的广泛应用

CRP不仅适用于AGI，还在科学和社会的广泛领域中具有重要应用。以下是CRP在不同领域中的应用示例。

医疗领域：在医疗领域，AI系统被广泛应用于诊断和治疗决策。CRP揭示了AI在处理等价医疗问题时的局限性。例如，AI系统在处理不同表述的相同病症时，可能会产生不同的诊断结果。通过引入‘I don’t know’函数，AI系统可以在无法确定诊断时选择“放弃”，从而提高其可信赖性。

金融领域：在金融领域，AI系统被用于风险评估和投资决策。CRP揭示了AI在处理等价金融问题时的挑战。例如，AI系统在处理不同表述的相同投资策略时，可能会产生不同的评估结果。通过引入‘I don’t know’函数，AI系统可以在无法确定评估结果时选择“放弃”，从而提高其可信赖性。

工程领域：在工程领域，AI系统被用于设计和优化工程方案。CRP揭示了AI在处理等价工程问题时的局限性。例如，AI系统在处理不同表述的相同设计方案时，可能会产生不同的优化结果。通过引入‘I don’t know’函数，AI系统可以在无法确定优化结果时选择“放弃”，从而提高其可信赖性。

公共管理领域：在公共管理领域，AI系统被用于政策制定和公共服务优化。CRP揭示了AI在处理等价公共管理问题时的挑战。例如，AI系统在处理不同表述的相同政策方案时，可能会产生不同的建议。通过引入‘I don’t know’函数，AI系统可以在无法确定建议时选择“放弃”，从而提高其可信赖性。

可信赖AI与‘I don’t know’函数的关系

CRP强调了构建可信赖AI的关键在于引入‘I don’t know’函数。具体来说，可信赖AI与‘I don’t know’函数的关系包括以下几点：

• 避免错误答案：通过引入‘I don’t know’函数，AI系统可以在无法确定答案时选择“放弃”，从而避免生成错误答案。这不仅提高了AI系统的可信赖性，也增强了用户对AI系统的信任。
• 提高系统透明度：‘I don’t know’函数使AI系统能够承认自身的局限性，并在必要时选择“放弃”。这提高了系统的透明度，使用户能够更好地理解AI系统的行为和决策过程。
• 增强系统鲁棒性：通过引入‘I don’t know’函数，AI系统可以在面对复杂和不确定的问题时，选择“放弃”而不是提供错误答案。这增强了系统的鲁棒性，使其能够在各种环境中稳定运行。
• 促进人机协作：‘I don’t know’函数使AI系统能够在无法确定答案时，寻求人类的帮助。这促进了人机协作，使AI系统能够更好地与人类合作，共同解决复杂问题。

构建可信赖AI的必要与充分条件

在构建可信赖的人工智能（AI）系统时，理解其必要与充分条件至关重要。论文通过一致性推理悖论（CRP）的研究，揭示了构建可信赖AI的关键因素，并提出了‘I don’t know’函数作为解决方案。

构建可信赖AI的必要条件包括以下几个方面。

一致性推理的局限性：CRP指出，任何试图进行一致性推理的AI都会不可避免地出现错误。这意味着，AI在模仿人类智能时，必须面对这种内在的局限性。因此，构建可信赖AI的第一个必要条件是承认一致性推理的局限性，并在设计系统时考虑到这一点。

‘I don’t know’功能：为了避免生成错误答案，AI系统必须具备在无法确定答案时说“I don’t know”的能力。这需要AI隐式计算一个新的概念，即‘I don’t know’函数。通过引入这一功能，AI可以在无法确定答案时选择“放弃”，从而提高其可信赖性。

透明度和可解释性：可信赖的AI系统不仅需要提供正确答案，还需要能够解释其答案的逻辑过程。这意味着，AI系统在提供答案时，必须具备一定的透明度和可解释性，使用户能够理解其决策过程。

鲁棒性和稳定性：可信赖的AI系统必须在各种环境中稳定运行，并能够应对复杂和不确定的问题。这需要系统具备一定的鲁棒性，能够在面对挑战时保持稳定。

在满足必要条件的基础上，构建可信赖AI的充分条件包括以下几个方面。

问题分类与分域处理：为了提高系统的可信赖性，可以将问题集合分为多个子域，并为每个子域建立特定的‘I don’t know’函数。例如，通过提示将问题集合分为多个子域，每个子域建立特定的‘I don’t know’函数。这种方法可以提高系统在特定领域内的可信赖性。

随机算法与确定性算法的结合：虽然随机算法在检测AI错误方面的效果有限，但通过结合随机算法与确定性算法，可以提高系统的可信赖性。例如，可以设计一个随机算法来检测AI的错误，并结合确定性算法来验证其结果，从而提高系统的准确性和可信赖性。

人机协作：通过引入人机协作机制，AI系统可以在无法确定答案时，寻求人类的帮助。这不仅可以提高系统的可信赖性，还可以增强用户对系统的信任。例如，当AI系统无法确定答案时，可以提示用户寻求人类专家的帮助，从而提高系统的决策质量。

持续学习与优化：可信赖的AI系统需要具备持续学习和优化的能力。通过不断学习和优化，系统可以逐步提高其决策质量和可信赖性。例如，可以通过引入机器学习和深度学习算法，使系统能够在不断积累数据的过程中，逐步提高其决策能力和准确性。

‘I don’t know’函数的计算与应用

‘I don’t know’函数是构建可信赖AI的关键。以下是‘I don’t know’函数的计算与应用：

‘I don’t know’函数的定义：‘I don’t know’函数用于将问题集合分为两部分：可以回答的问题（Ωknow）和无法回答的问题（Ωdon’t know）。具体来说，‘I don’t know’函数ΞI将这些问题进行分类，其中ΞI(ι) = 1表示AI无法回答的问题，ΞI(ι) = 0表示AI可以回答的问题。

‘I don’t know’函数的计算：为了计算‘I don’t know’函数，可以采用以下方法：

将问题集合分为多个子域，并为每个子域建立特定的‘I don’t know’函数。例如，通过提示将问题集合分为多个子域，每个子域建立特定的‘I don’t know’函数。

结合随机算法与确定性算法，可以提高‘I don’t know’函数的计算准确性。例如，可以设计一个随机算法来检测AI的错误，并结合确定性算法来验证其结果，从而提高‘I don’t know’函数的计算准确性。

通过持续学习和优化，可以逐步提高‘I don’t know’函数的计算准确性。例如，可以通过引入机器学习和深度学习算法，使系统能够在不断积累数据的过程中，逐步提高‘I don’t know’函数的计算准确性。

‘I don’t know’函数在构建可信赖AI系统中具有广泛的应用。例如：

• 医疗领域：在医疗领域，AI系统可以通过‘I don’t know’函数，在无法确定诊断时选择“放弃”，从而提高诊断的准确性和可信赖性。
• 金融领域：在金融领域，AI系统可以通过‘I don’t know’函数，在无法确定评估结果时选择“放弃”，从而提高风险评估和投资决策的准确性和可信赖性。
• 工程领域：在工程领域，AI系统可以通过‘I don’t know’函数，在无法确定优化结果时选择“放弃”，从而提高设计和优化方案的准确性和可信赖性。
• 公共管理领域：在公共管理领域，AI系统可以通过‘I don’t know’函数，在无法确定政策建议时选择“放弃”，从而提高政策制定和公共服务优化的准确性和可信赖性。

图片

图6:AGI的失败句——给定AGI处理基本算术的代码部分。给定一个AGI（总是回答）通过一致的推理来模拟人类智能，在上述问题上会失败。请注意，只需要访问处理基本算术的AGI代码（CodeAGI）。维度d=dkdk-1。d1，其中dk-1。d1在0和9之间，dk在1和9之间。例如，d=2024。上述句子的长度（字符数）以长度（CodeAGI）+3300+k为界。代码generateA使用CodeAGI以特定方式创建线性程序中矩阵A的近似值，详见补充材料。

SCI层次结构、优化与哥德尔不完备定理的联系

一致性推理悖论（CRP）的提出不仅揭示了AI在模仿人类智能时的内在挑战，还展示了其在科学理论中的深远影响。论文通过SCI层次结构、优化问题和哥德尔不完备定理的联系，深入探讨CRP的理论基础和应用。

SCI（Solvability Complexity Index）层次结构是一个用于分类计算问题复杂性的理论框架。它推广了经典的算术层次结构，包含了递归理论和计算复杂性理论的核心概念。SCI层次结构的主要目的是通过引入新的分类方法，来描述和分析计算问题的可解性和复杂性。

在SCI层次结构中，问题被分类为不同的层次，每个层次代表不同的计算复杂性。例如，Σ1类问题是那些可以通过一个极限计算的函数，而∆1类问题则是可以通过计算函数直接解决的问题。SCI层次结构不仅包含了这些经典的分类，还引入了新的分类方法，如相变理论和随机算法，以更全面地描述计算问题的复杂性。

SCI层次结构的一个重要特点是它能够处理连续优化问题和计算光谱理论中的复杂性。这使得SCI层次结构成为研究一致性推理悖论和构建可信赖AI系统的重要工具。

一致性推理悖论在优化问题中具有广泛的应用。优化问题是科学和工程中的核心问题，涉及到在给定约束条件下寻找最优解。常见的优化问题包括线性规划、基追踪和LASSO等。这些问题在医疗、金融、工程和公共管理等领域中具有重要应用。

CRP在优化问题中的应用主要体现在以下几个方面：

• 线性规划：线性规划是优化问题中的一种基本形式，涉及到在给定约束条件下寻找线性目标函数的最优解。CRP揭示了AI在处理等价线性规划问题时的局限性。例如，AI系统在处理不同表述的相同线性规划问题时，可能会产生不同的优化结果。通过引入‘I don’t know’函数，AI系统可以在无法确定优化结果时选择“放弃”，从而提高其可信赖性。
• 基追踪：基追踪是一种用于信号处理和数据压缩的优化技术，涉及到在给定约束条件下寻找稀疏解。CRP揭示了AI在处理等价基追踪问题时的挑战。例如，AI系统在处理不同表述的相同基追踪问题时，可能会产生不同的优化结果。通过引入‘I don’t know’函数，AI系统可以在无法确定优化结果时选择“放弃”，从而提高其可信赖性。
• LASSO：LASSO是一种用于回归分析的优化技术，涉及到在给定约束条件下寻找最优回归系数。CRP揭示了AI在处理等价LASSO问题时的局限性。例如，AI系统在处理不同表述的相同LASSO问题时，可能会产生不同的优化结果。通过引入‘I don’t know’函数，AI系统可以在无法确定优化结果时选择“放弃”，从而提高其可信赖性。

哥德尔不完备定理是数学和逻辑领域中的一个重要理论，揭示了在任何一致且足够复杂的形式系统中，存在一些命题既无法被证明为真，也无法被证明为假。哥德尔不完备定理对计算理论和AI研究具有深远影响。

CRP与哥德尔不完备定理有着密切的联系。具体来说，CRP IV提供了一个类似于哥德尔第一不完备定理的声明，专门针对优化问题。这意味着，在某些优化问题中，AI可能无法提供逻辑上正确的解释，即使其答案是正确的。这一发现揭示了AI在处理复杂问题时的内在局限性，并强调了构建可信赖AI系统的挑战。

此外，CRP还展示了在特定问题集合上存在不会产生幻觉且总是正确的AI，但如果AI试图通过一致性推理模仿人类智能，则不可避免地会出现错误。这与哥德尔不完备定理的核心思想相呼应，即在任何一致且足够复杂的系统中，存在无法解决的问题。

经典递归理论是计算理论的基础，研究可计算函数和不可计算问题。图灵的停机问题是递归理论中的一个经典问题，揭示了某些问题无法通过算法解决。具体来说，停机问题指出，无法设计一个算法来确定任意计算机程序是否会停止运行。

CRP展示了AI在处理可计算问题时的局限性，强调了经典递归理论在理解AI系统行为中的重要性。具体来说，CRP指出，任何试图进行一致性推理的AI都会不可避免地出现错误。这意味着，AI在模仿人类智能时，必须面对这种内在的局限性。

此外，CRP还展示了在特定问题集合上存在不会产生幻觉且总是正确的AI，但如果AI试图通过一致性推理模仿人类智能，则不可避免地会出现错误。这与经典递归理论的核心思想相呼应，即在任何一致且足够复杂的系统中，存在无法解决的问题。

图片

图7:CRP与Claude的实践。图3和图4中聊天机器人Claude的实验（略有修改）。

ChatGPT和Gemini的成功和失败是一样的。

CRP对AI发展的启示

一致性推理悖论（CRP）不仅揭示了AI在模仿人类智能时的内在挑战，还为未来AI的发展提供了重要的启示。论文通过分析一致性推理的局限性、‘I don’t know’功能的重要性、可信赖AI的设计原则、多领域应用的潜力、随机算法的局限性以及经典递归理论的应用，探讨CRP对AI发展的深远影响。

一致性推理的局限性

一致性推理是人类智能的核心能力之一，指的是处理等价但表述不同的任务的能力。然而，CRP揭示了AI在模仿这种能力时的内在局限性。具体来说，任何试图进行一致性推理的AI都会不可避免地出现错误。这些错误不仅仅是偶然的，而是在某些问题上会无限次发生。

这种现象的根本原因在于，AI在处理等价问题时，无法始终提供一致且正确的答案。即使AI具备强大的计算能力和存储能力，它在面对等价问题时，仍然会出现错误。这一发现促使我们重新思考AI系统在模仿人类智能时的局限性，并探索如何设计更可信赖的AI系统。

‘I don’t know’功能的重要性

为了构建可信赖的AI系统，‘I don’t know’功能至关重要。具体来说，‘I don’t know’功能使AI系统能够在无法确定答案时选择“放弃”，从而避免生成错误答案。这不仅提高了AI系统的可信赖性，也增强了用户对AI系统的信任。

‘I don’t know’功能的重要性体现在以下几个方面：

• 避免错误答案：通过引入‘I don’t know’功能，AI系统可以在无法确定答案时选择“放弃”，从而避免生成错误答案。这不仅提高了AI系统的可信赖性，也增强了用户对AI系统的信任。
• 提高系统透明度：‘I don’t know’功能使AI系统能够承认自身的局限性，并在必要时选择“放弃”。这提高了系统的透明度，使用户能够更好地理解AI系统的行为和决策过程。
• 增强系统鲁棒性：通过引入‘I don’t know’功能，AI系统可以在面对复杂和不确定的问题时，选择“放弃”而不是提供错误答案。这增强了系统的鲁棒性，使其能够在各种环境中稳定运行。
• 促进人机协作：‘I don’t know’功能使AI系统能够在无法确定答案时，寻求人类的帮助。这促进了人机协作，使AI系统能够更好地与人类合作，共同解决复杂问题。

可信赖AI的设计原则

在构建可信赖AI系统时，需要遵循以下设计原则。

CRP指出，任何试图进行一致性推理的AI都会不可避免地出现错误。因此，构建可信赖AI的第一个原则是承认一致性推理的局限性，并在设计系统时考虑到这一点。

为了避免生成错误答案，AI系统必须具备在无法确定答案时说“I don’t know”的能力。这需要AI隐式计算一个新的概念，即‘I don’t know’函数。通过引入这一功能，AI可以在无法确定答案时选择“放弃”，从而提高其可信赖性。

可信赖的AI系统不仅需要提供正确答案，还需要能够解释其答案的逻辑过程。这意味着，AI系统在提供答案时，必须具备一定的透明度和可解释性，使用户能够理解其决策过程。

可信赖的AI系统必须在各种环境中稳定运行，并能够应对复杂和不确定的问题。这需要系统具备一定的鲁棒性，能够在面对挑战时保持稳定。

为了提高系统的可信赖性，可以将问题集合分为多个子域，并为每个子域建立特定的‘I don’t know’函数。例如，通过提示将问题集合分为多个子域，每个子域建立特定的‘I don’t know’函数。这种方法可以提高系统在特定领域内的可信赖性。

虽然随机算法在检测AI错误方面的效果有限，但通过结合随机算法与确定性算法，可以提高系统的可信赖性。例如，可以设计一个随机算法来检测AI的错误，并结合确定性算法来验证其结果，从而提高系统的准确性和可信赖性。

可信赖的AI系统需要具备持续学习和优化的能力。通过不断学习和优化，系统可以逐步提高其决策质量和可信赖性。例如，可以通过引入机器学习和深度学习算法，使系统能够在不断积累数据的过程中，逐步提高其决策能力和准确性。

多领域应用的潜力

CRP不仅适用于AGI，还在科学和社会的广泛领域中具有重要应用。以下是CRP在不同领域中的应用示例：

在医疗领域，AI系统被广泛应用于诊断和治疗决策。CRP揭示了AI在处理等价医疗问题时的局限性。例如，AI系统在处理不同表述的相同病症时，可能会产生不同的诊断结果。通过引入‘I don’t know’函数，AI系统可以在无法确定诊断时选择“放弃”，从而提高其可信赖性。

在金融领域，AI系统被用于风险评估和投资决策。CRP揭示了AI在处理等价金融问题时的挑战。例如，AI系统在处理不同表述的相同投资策略时，可能会产生不同的评估结果。通过引入‘I don’t know’函数，AI系统可以在无法确定评估结果时选择“放弃”，从而提高其可信赖性。

在工程领域，AI系统被用于设计和优化工程方案。CRP揭示了AI在处理等价工程问题时的局限性。例如，AI系统在处理不同表述的相同设计方案时，可能会产生不同的优化结果。通过引入‘I don’t know’函数，AI系统可以在无法确定优化结果时选择“放弃”，从而提高其可信赖性。

在公共管理领域，AI系统被用于政策制定和公共服务优化。CRP揭示了AI在处理等价公共管理问题时的挑战。例如，AI系统在处理不同表述的相同政策方案时，可能会产生不同的建议。通过引入‘I don’t know’函数，AI系统可以在无法确定建议时选择“放弃”，从而提高其可信赖性。

随机算法的局限性

CRP III(b)指出，使用随机算法检测AI错误的成功概率不会超过50%。具体来说，即使设计一个随机算法来检测AI的错误，其成功概率也不会超过纯粹猜测的50%。这意味着，随机算法在检测AI错误方面的效果非常有限。

这一发现对现代AI系统，尤其是依赖随机算法的聊天机器人具有重要意义。它表明，不能完全依赖随机算法来保证AI系统的正确性，而需要引入其他机制，如‘I don’t know’功能，以提高系统的可信赖性。

经典递归理论的应用

经典递归理论是计算理论的基础，研究可计算函数和不可计算问题。图灵的停机问题是递归理论中的一个经典问题，揭示了某些问题无法通过算法解决。具体来说，停机问题指出，无法设计一个算法来确定任意计算机程序是否会停止运行。

CRP展示了AI在处理可计算问题时的局限性，强调了经典递归理论在理解AI系统行为中的重要性。具体来说，CRP指出，任何试图进行一致性推理的AI都会不可避免地出现错误。这意味着，AI在模仿人类智能时，必须面对这种内在的局限性。

此外，CRP还展示了在特定问题集合上存在不会产生幻觉且总是正确的AI，但如果AI试图通过一致性推理模仿人类智能，则不可避免地会出现错误。这与经典递归理论的核心思想相呼应，即在任何一致且足够复杂的系统中，存在无法解决的问题。

CRP对AI发展的启示包括承认一致性推理的局限性、引入‘I don’t know’功能、遵循可信赖AI的设计原则、探索多领域应用的潜力、认识随机算法的局限性以及应用经典递归理论。通过深入理解和应用CRP，我们可以在未来的AI研究和应用中，设计出更智能、更可信赖的系统。（END）

参考资料：https://arxiv.org/pdf/2408.02357

本文转载自 ​​大噬元兽​​，作者： FlerkenS