超越GPT-4！香港科技大学破解Transformer算术难题，乘法准确率超99.9% 精华

探索Transformer在算术问题中的局限性

在近年来的自然语言处理领域，基于Transformer的大型语言模型（LLMs）取得了显著的成就。然而，当这些模型被应用到看似简单的算术问题上时，它们常常表现出意外的挣扎，尤其是在处理基本的整数乘法任务时。例如，尽管GPT-4等现代LLM在多种任务中表现出色，但在执行简单的整数乘法时却遇到了困难。这种明显的能力差异引发了人们对于这些模型安全和伦理使用的担忧，并阻碍了它们的广泛应用。

本文旨在通过探索和解释Transformer在整数乘法任务中的不足，来深入理解这些模型在算术问题上的局限性。我们通过对一个标准Transformer模型在n位整数乘法任务中的表现进行全面分析，揭示了模型在处理连续进位和缓存中间结果时的困难，并通过实验验证了这些推论。基于这些发现，我们提出了改进措施，以提升Transformer在乘法任务上的性能。这些改进不仅增强了模型的解释性，还通过严格的测试和数学建模得到了验证，例如，在5位整数乘法任务上，我们实现了超过99.9%的准确率，超过了GPT-4等大型语言模型。

论文标题：Dissecting Multiplication in Transformers: Insights into LLMs

机构：

1. Hong Kong University of Science and Technology
2. Hong Kong Polytechnic University

论文链接：​​https://arxiv.org/pdf/2407.15360.pdf​​

通过本研究，我们不仅提升了对Transformer模型在处理复杂算术任务中的理解，也为AI的安全性和可靠性研究提供了新的视角和方法论，推动了可解释AI（XAI）的发展，帮助构建了对大型语言模型的信任，并促进了它们在关键应用中的采用。

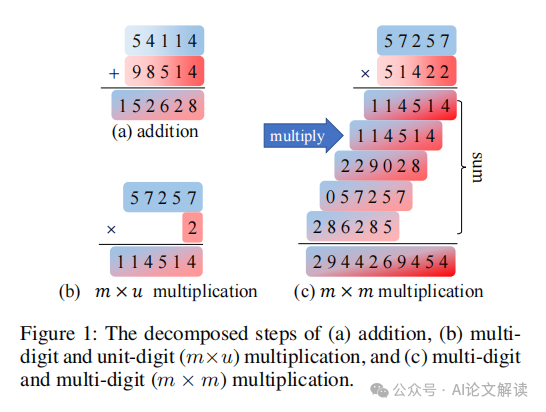
Transformer模型在算术任务中的表现

Transformer模型在自然语言处理任务中取得了显著的成就，但在算术任务，尤其是整数乘法方面，它们的表现却常常不尽人意。尽管Transformer拥有庞大的模型能力，它在处理简单的整数乘法任务时却表现出明显的挑战。这种能力的不对等引起了人们对其安全和道德使用的关注，并阻碍了其广泛的应用。

在本文中，我们专注于整数乘法任务，探索和解释Transformer在这一领域的不完美表现。我们对一个基本的Transformer模型进行了全面分析，该模型被训练用于执行n位整数乘法。我们的观察表明，模型将乘法任务分解为多个并行的子任务，每个子任务针对每个数字顺序优化，以完成最终的乘法计算。

基础乘法分析：单位数乘法

在对Transformer在m×u（多位数乘以单位数）乘法任务的表现进行分析时，我们发现Transformer利用几个基本子任务来完成乘法计算。这些子任务包括：

基本乘法（BM）：BM计算两个单个数字在每个位置的乘积。根据是否产生进位到下一个位置，BM可以分为BM（带进位）和BM（不带进位）。

使用进位（UC）：UC考虑前一个数字的进位，并将进位加到当前位置的乘积上。

基于上述基本子任务，Transformer可以将多个子任务链接在一起，实现复杂的功能，例如使用进位和进一步进位（UCFC），考虑来自前一列的进位，并进一步产生到下一列的进位。

总体分析

我们首先调查Transformer如何学习每个子任务。通过观察每个数字的训练损失，我们发现Transformer似乎是半独立地学习每个答案数字的。单位数字（A0）和最高位数字（A5）的学习速度比其他数字快，且噪声更少。这是因为A0的计算不需要考虑进位，从而简化了计算过程。与A0相比，A5的计算只需要考虑进位。

每个任务的分析

我们进一步分析每个子任务的训练数据，将训练数据分为与每个子任务对应的不重叠子集，并分别展示每个子任务的每个数字的损失曲线。从BM（不带进位）和BM（带进位）的训练曲线可以看出，所有任务开始时损失都很高。随着训练的进行，所有损失曲线都有所下降，但不同任务之间存在“时间滞后”。BM（不带进位）的损失下降最快，这是因为它是所有其他任务的基础，必须先准确计算才能进行后续计算。BM（带进位）和进位损失的下降速度是第二快的，这两个子任务是互补的计算，它们的收敛表明模型能够准确计算进位。UC的损失在训练初期表现出显著的平台期，这符合我们的预期，即UC子任务需要准确计算进位，因此UC的损失只有在进位任务收敛后才能下降。UCFC的损失下降最晚，因为UCFC的计算跨越3个数字，即当前数字的乘积、前一个数字的进位和向下一个数字的进位，因此其收敛发生在所有其他损失收敛之后。

从这些分析中，我们可以看出，尽管Transformer在处理简单的单位数乘法任务时表现出一定的能力，但在更复杂的多位数乘法任务中，其性能急剧下降，显示出明显的不足。这些发现为理解和改进Transformer模型在算术任务中的表现提供了宝贵的见解。

多位数乘法的深入分析

在探讨多位数乘法的处理中，我们发现转换器（transformer）在执行这一任务时会将其分解为多个子任务，并行计算。这些子任务包括基本的数字乘法（Base Multiply, BM），使用进位（Use Carry, UC），以及进一步的进位处理（Further Carry, UCFC）。通过对这些子任务的深入分析，我们可以更好地理解转换器在处理多位数乘法时的行为模式及其局限性。

基本乘法和进位处理

在多位数乘法中，转换器首先处理基本的数字乘法，即单个数字间的乘法。这一步骤相对简单，但关键在于如何处理和传递进位。例如，在乘法​​47134 × 9​​中，每一位数字与9相乘后的结果需要考虑前一位的进位，这增加了计算的复杂性。转换器在这一过程中展示了分阶段学习的特点，即先学习无需进位的乘法，然后逐渐学习如何处理进位。

子任务的学习顺序

通过观察损失曲线，我们发现转换器在学习各个子任务时存在顺序性。基本的乘法（BM）通常是最先被学习的，因为它是其他计算的基础。随后，转换器学习如何处理进位（UC），最后是更复杂的进位传递（UCFC）。这种学习顺序反映了任务的内在复杂性和依赖关系。

提出改进措施

基于上述分析，我们提出以下几点改进措施，以增强转换器在多位数乘法任务上的表现：

1. 反转答案数字

研究表明，将答案数字反转（即从低位到高位进行计算）可以显著提高模型的准确率。这种方法模仿了人类计算乘法的习惯，从而使得模型能够更有效地利用已生成的低位数字来预测高位数字。

2. 增加模型深度

多位数乘法涉及复杂的中间步骤和多层次的计算，增加模型的深度可以提供更多的层次来处理这些中间结果，从而提高准确性。实验表明，增加深度能够显著提升模型在处理多位数乘法时的表现。

3. 增加简单样本的比例

在训练初期增加简单样本（如单一位数乘法）的比例，可以帮助模型在学习更复杂的多位数乘法前，先掌握基本的乘法规则。这种渐进式学习策略可以减少学习难度，提高模型的整体性能。

通过实施这些改进措施，我们能够显著提高转换器在多位数乘法任务上的准确率和效率，从而推动其在更广泛的应用场景中的部署和使用。

实验验证与结果分析

1. 实验设计与方法

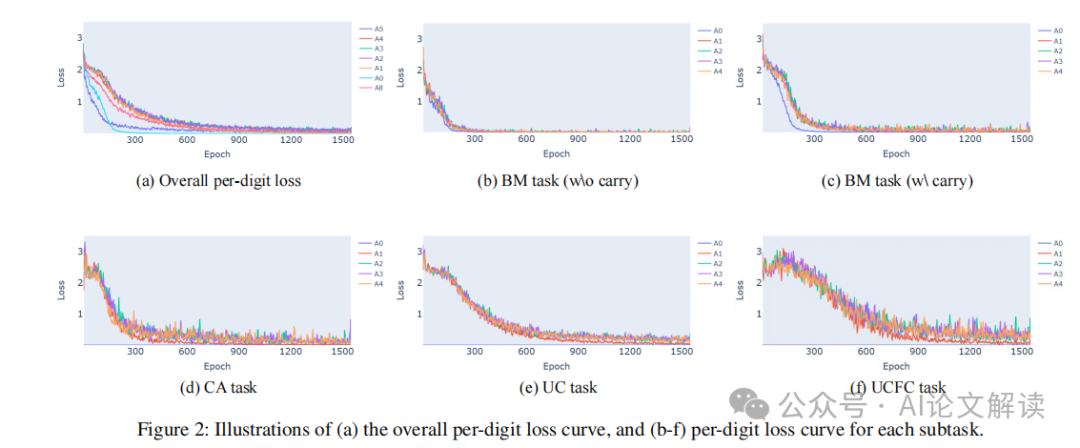
本研究通过实验验证了Transformer在整数乘法任务上的性能。我们首先使用单层解码器仅Transformer模型在m × u（多位数乘以单位数）乘法任务上进行训练，并逐步扩展到多层Transformer模型在m × m（多位数乘以多位数）乘法任务上的训练。实验中，每个数字在训练数据中独立采样自均匀分布{0,1,...,9}。我们使用Adam优化器，学习率设置为1e-4。

2. 实验结果

实验结果显示，在m × u乘法任务上，Transformer模型能够通过学习不同的子任务（如基础乘法、使用进位等）逐步提高预测的准确性。然而，在扩展到更复杂的m × m乘法任务时，模型的准确率显著下降。这表明单层Transformer模型在处理包含多个中间步骤的复杂任务时存在局限性。

3. 结果分析

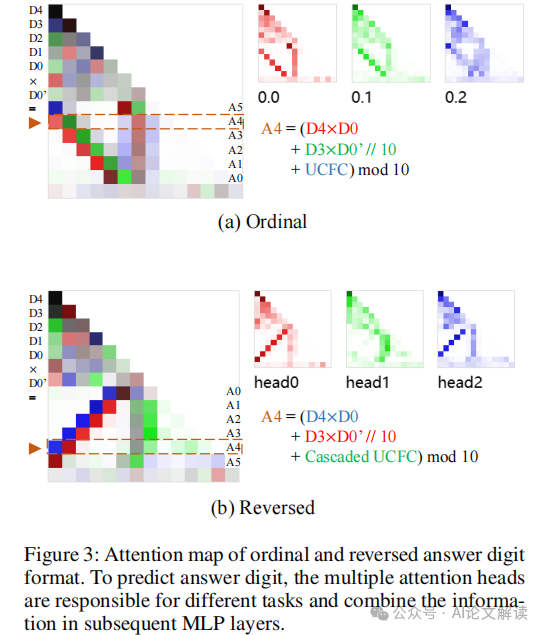
通过对不同子任务的训练损失进行分析（如图2所示），我们观察到不同子任务的学习速度存在显著差异。基础乘法（BM）任务的损失下降最快，而涉及多个计算步骤的子任务（如使用进位和进一步进位的计算）的损失下降较慢。这些观察结果支持了我们的假设，即Transformer在处理复杂的算术任务时，其性能受限于对中间计算结果的处理能力。

本文转载自​​​AI论文解读​​