中科大联合华为诺亚提出Entropy Law,揭秘大模型性能、数据压缩率以及训练损失关系
本工作由中科大认知智能全国重点实验室 IEEE Fellow 陈恩红团队与华为诺亚方舟实验室完成。陈恩红教授团队深耕数据挖掘、机器学习领域,在顶级期刊与会议上发表多篇论文,谷歌学术论文引用超两万次。诺亚方舟实验室是华为公司从事人工智能基础研究的实验室,秉持理论研究与应用创新并重的理念,致力于推动人工智能领域的技术创新和发展。
数据是大语言模型(LLMs)成功的基石,但并非所有数据都有益于模型学习。直觉上,高质量的样本在教授 LLM 上预期会有更好的效率。因此,现有方法通常专注于基于质量的数据选择。然而,这些方法中的大多数独立地评估不同的数据样本,忽略了样本之间复杂的组合效应。如图 1 所示,即使每个样本质量完美,由于它们的互信息冗余或不一致性,它们的组合可能仍然次优。尽管基于质量的子集由所有三个优质样本组成,但它们编码的知识实际上是冗余和冲突的。相比之下,另一个由几个相对较低质量但多样化的样本组成的数据子集在教授 LLM 方面可能传达更多信息。因此,基于质量的数据选择并未完全符合最大化 LLM 知识掌握的目标。
而本文旨在揭示 LLM 性能与数据选择之间的内在关系。受 LLM 信息压缩本质的启发,我们发现了一条 entropy law,它将 LLM 性能与数据压缩率和前几步模型训练的损失加以联系,分别反映了数据集的信息冗余程度和 LLM 对数据集中固有知识的掌握程度。通过理论推导和实证评估,我们发现模型性能与训练数据的压缩率呈负相关,而这通常会产生较低的训练损失。基于 entropy law 的发现,我们提出了一种非常高效且通用的数据选择方法用于训练 LLM,名为 ZIP,其旨在优先选择低压缩率的数据子集。ZIP 分多阶段、贪心地选择多样化的数据,最终获得一个具有良好多样性的数据子集。

- 团队:中科大认知智能全国重点实验室陈恩红团队,华为诺亚方舟实验室
- 论文链接: https://arxiv.org/pdf/2407.06645
- 代码链接: https://github.com/USTC-StarTeam/ZIP
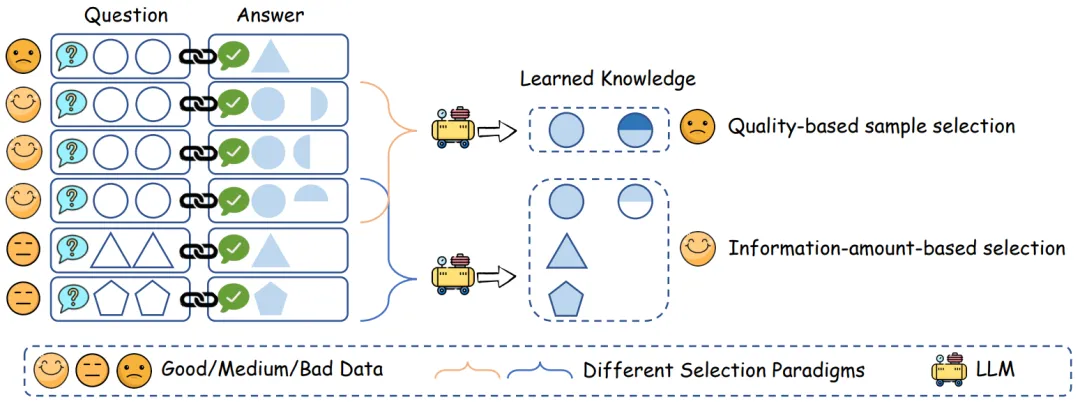
图 1
Entropy law
我们对数据压缩与 LLM 性能之间的关系进行理论分析。直觉上,训练数据的正确性和多样性会影响最终模型的性能。同时,如果数据存在严重的内在冲突或模型对数据编码的信息掌握不佳,LLM 的性能可能会次优。基于这些假设,我们将 LLM 的性能表示为 Z ,其预期会受到以下因素的影响:
- 数据压缩率 R:直觉上,压缩率越低的数据集表明信息密度越高。
- 训练损失 L:表示数据对模型来说是否难以记忆。在相同的基础模型下,高训练损失通常是由于数据集中存在噪声或不一致的信息。
- 数据一致性 C:数据的一致性通过给定前文情况下下一个 token 的概率的熵来反映。更高的数据一致性通常会带来更低的训练损失。
- 平均数据质量 Q:反映了数据的平均样本级质量,可以通过各种客观和主观方面来衡量。
给定一定量的训练数据,模型性能可以通过上述因素来估计:
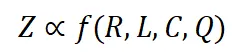
其中 f 是一个隐函数。给定一个特定的基础模型,L 的规模通常取决于 R 和 C,可以表示为:
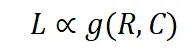
由于具有更高同质性或更好数据一致性的数据集更容易被模型学习,L 预计在 R 和 C 上是单调的。因此,我们可以将上述公式重写为:
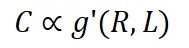
其中 g' 是一个反函数。通过结合上述三个方程,我们得到:
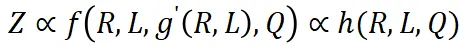
其中 h 是另一个隐函数。如果数据选择方法不会显著改变平均数据质量 Q,我们可以近似地将变量 Q 视为常数。因此,最终性能可以粗略地表示为:
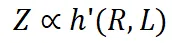
这意味着模型性能与数据压缩率和训练损失相关。我们将这种关系称为 Entropy law。
基于 Entropy law,我们提出两个推论:
- 如果将 C 视为常数,训练损失直接受压缩率影响。因此,模型性能由压缩率控制:如果数据压缩率 R 较高,那么 Z 通常较差,这将在我们的实验中得到验证。
- 在相同的压缩率下,较高训练损失意味着较低的数据一致性。因此,模型学到的有效知识可能更有限。这可以用来预测 LLM 在具有相似压缩率和样本质量的不同数据上的性能。我们将在后续展示这一推论在实践中的应用。
ZIP:高度轻量化的数据选择算法
在 entropy law 的指导下,我们提出了 ZIP 这一数据选择方法,通过数据压缩率来选择数据样本,旨在在有限的训练数据预算下最大化有效信息量。出于效率考量,我们采用了一种迭代多阶段贪心范式,以高效地获得具有相对低压缩率的近似解。在每轮迭代中,我们首先使用全局选择阶段来选择一组具有低压缩率的候选样本池,找到信息密度高的样本。然后,我们采用粗粒度的局部选择阶段,选择一组与已选样本冗余度最低的较小样本集。最后,我们使用细粒度的局部选择阶段,最小化要添加样本之间的相似性。上述过程持续进行直到获得足够的数据,具体算法如下:

实验结果
1.ZIP 选择算法对于不同 LLM、在不同 LLM 对齐阶段的有效性
对比不同的 SFT 数据选择算法,基于 ZIP 选择数据所训练得到的模型性能上展现出优势,并且在效率上也占优。具体结果见下表:
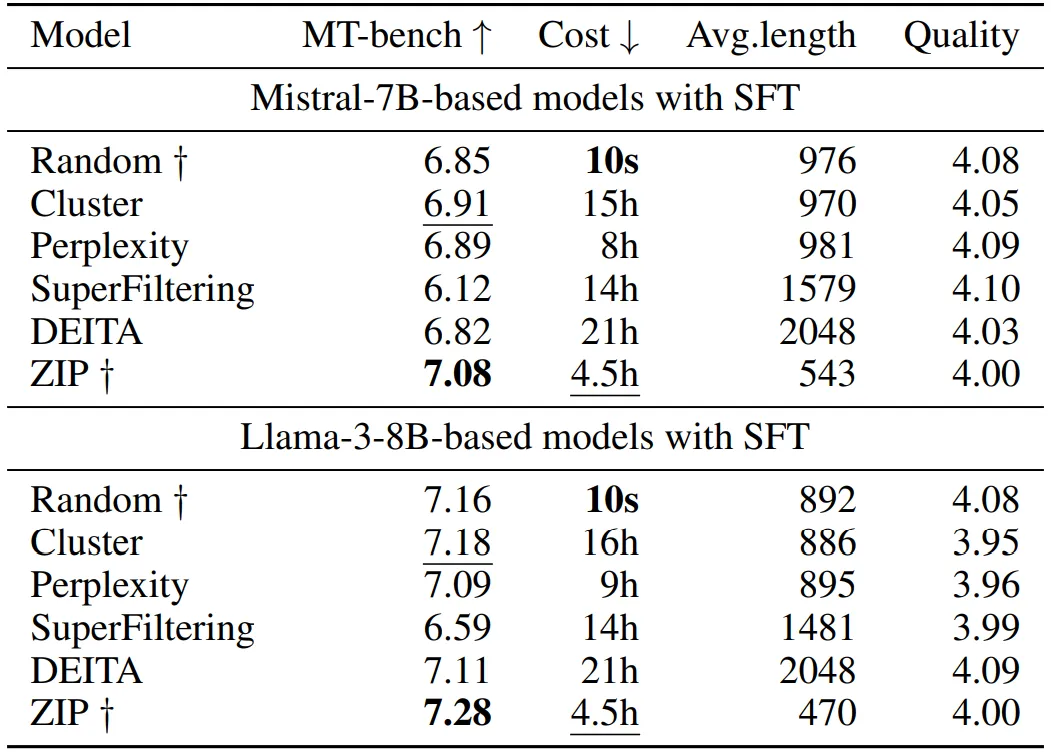
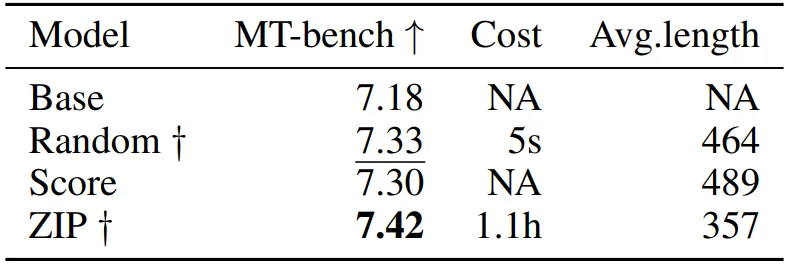
2.Entropy law 的实验验证
基于 SFT 数据选择实验,我们基于模型效果、数据压缩率以及模型在前几步训练的损失,分别拟合了多条关系曲线。结果见图 2 以及图 3,我们从图中可以观察到三个因素之间的紧密关联。首先,低压缩率数据通常会带来更好的模型效果,这是因为 LLMs 的学习过程与信息压缩高度相关,我们可以将 LLM 视为数据压缩器,那么压缩率较低的数据意味着更多的知识量,从而对压缩器更有价值。同时,可以观察到较低的压缩率通常伴随着更高的训练损失,这是因为难以压缩的数据携带了更多的知识,对 LLM 吸收其中蕴含的知识提出了更大的挑战。
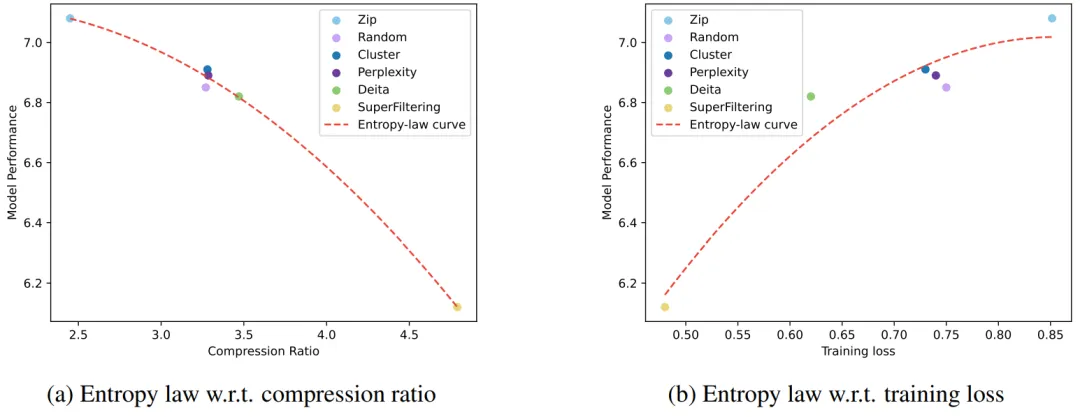
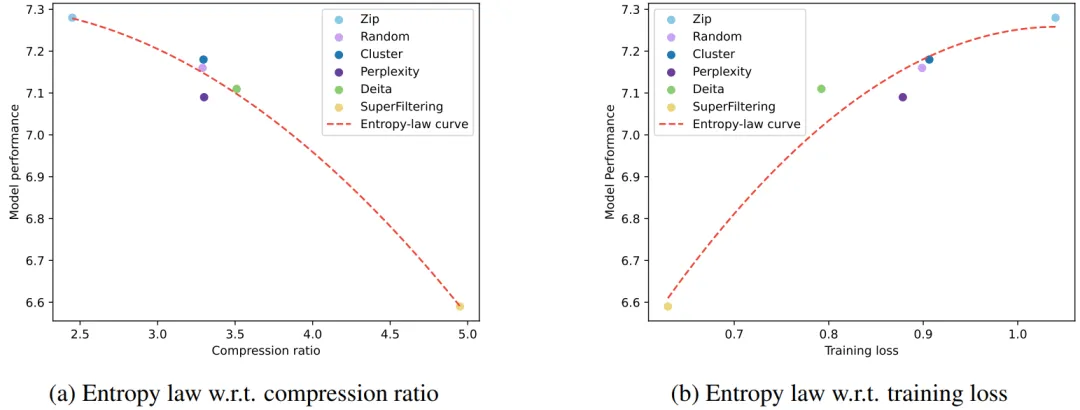
图 3 Llama-3-8B
3.Entropy law 的实际应用
我们提供了一个 entropy law 在真实场景中指导 LLM 训练数据增量更新的应用。在该任务场景中,训练数据量保持相对稳定,只有一小部分数据会被修改。结果见图 4,其中
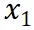
到
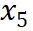
是逐渐增量更新的 5 个数据版本,出于保密要求,仅提供不同压缩率下模型效果的相对关系。根据 entropy law 预测,假设每次增量更新后数据质量没有显著下降,可以预期随着数据压缩率的降低,模型性能会有所提升。这一预测与图中数据版本
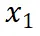
到
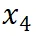
的结果一致。然而,数据版本
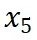
显示出损失和数据压缩率的异常增加,这预示了由于训练数据一致性下降导致的模型性能下降的潜在可能。这一预测通过随后的模型性能评估进一步得到证实。因此,entropy law 可以作为 LLM 训练的指导原则,无需在完整数据集上训练模型直到收敛,便可预测 LLM 训练失败的潜在风险。鉴于训练 LLM 的高昂成本,这一点尤其重要。
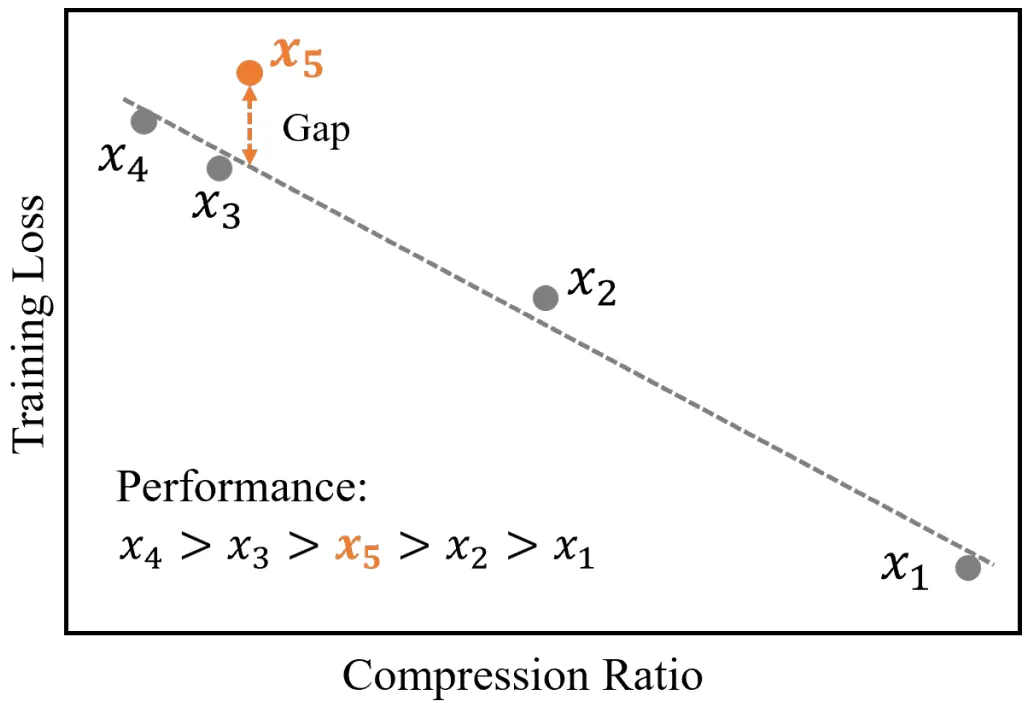
图 4
本文转自 机器之心 ,作者:机器之心

















