思维树：利用大型语言模型深思熟虑地解决问题 原创

摘要：语言模型正越来越多地用于广泛任务中的一般问题解决，但在推理过程中，它们仍然局限于逐字级别、从左到右的决策过程。这意味着它们在需要探索、战略性前瞻，或初始决策起关键作用的任务中可能表现不佳。为了解决这些挑战，我们引入了一种新的语言模型推理框架——“思维树”（Tree of Thoughts，ToT），它推广了流行的“链式思维”方法，通过提示语言模型并使其能够探索作为解决问题中间步骤的连贯文本单元（“思想”）。ToT 允许语言模型通过考虑多种不同的推理路径并自我评估选择来进行深思熟虑的决策，决定下一步行动，同时在必要时前瞻或回溯以做出全局性选择。我们的实验表明，ToT 显著增强了语言模型在需要非平凡规划或搜索的三项新任务中的问题解决能力：24点游戏、创意写作和迷你填字游戏。例如，在24点游戏中，使用链式思维提示的GPT-4仅解决了4%的任务，而我们的方法达到了74%的成功率。所有提示的代码仓库： [https://github.com/princeton-nlp/tree-of-thought-llm](https://github.com/princeton-nlp/tree-of-thought-llm)。

1.引言

最初设计用于生成文本的大规模语言模型（LMs），如GPT和PaLM，已经被证明能够执行越来越多需要数学、符号、常识和知识推理的任务。或许令人惊讶的是，这些进步的基础仍然是原始的自回归机制，用于生成文本，即逐个令牌地从左到右做出决策。这样的简单机制是否足以构建一个通用问题解决器？如果不是，哪些问题会挑战当前的范式，应该采用哪些替代机制？

关于人类认知的文献提供了一些回答这些问题的线索。关于“二元过程”模型的研究表明，人们在做决定时有两种模式——一种是快速、自动、无意识的模式（“系统1”），另一种是慢速、深思熟虑、有意识的模式（“系统2”）。这些模式以前与机器学习中使用的各种数学模型相关联。例如，人类和其他动物的强化学习研究探讨了在什么情况下他们会进行联想的“无模型”学习或更深思熟虑的“基于模型”的规划。LMs的简单联想令牌级别选择也让人联想到“系统1”，因此可能受益于一个更深思熟虑的“系统2”规划过程的增强，该过程（1）保持并探索当前选择的多种替代方案，而不仅仅是选择一个，并且（2）评估其当前状态并积极前瞻或回溯以做出更全局的决策。

为了设计这样的规划过程，我们回到人工智能（和认知科学）的起源，从Newell、Shaw和Simon在20世纪50年代开始探索的规划过程中汲取灵感。Newell和同事将问题解决描述为在组合问题空间中的搜索，表示为树状结构。因此，我们提出了“思维树”（Tree of Thoughts，ToT）框架，以通过语言模型进行通用问题解决。如图1所示，现有方法（详见下文）采样用于问题解决的连续语言序列，而ToT则主动维护一个思想树，每个思想都是一个连贯的语言序列，作为问题解决的中间步骤。这样的高级语义单元允许LM通过一种深思熟虑的推理过程自我评估不同中间思想在解决问题方面的进展，这个过程也在语言中体现出来。通过LM自我评估和深思熟虑来实现搜索启发式是新颖的，因为以前的搜索启发式要么是编程的，要么是学习的。最后，我们将这种基于语言的生成和评估多样思想的能力与搜索算法（如广度优先搜索（BFS）或深度优先搜索（DFS））结合起来，允许系统地探索思想树，进行前瞻和回溯。

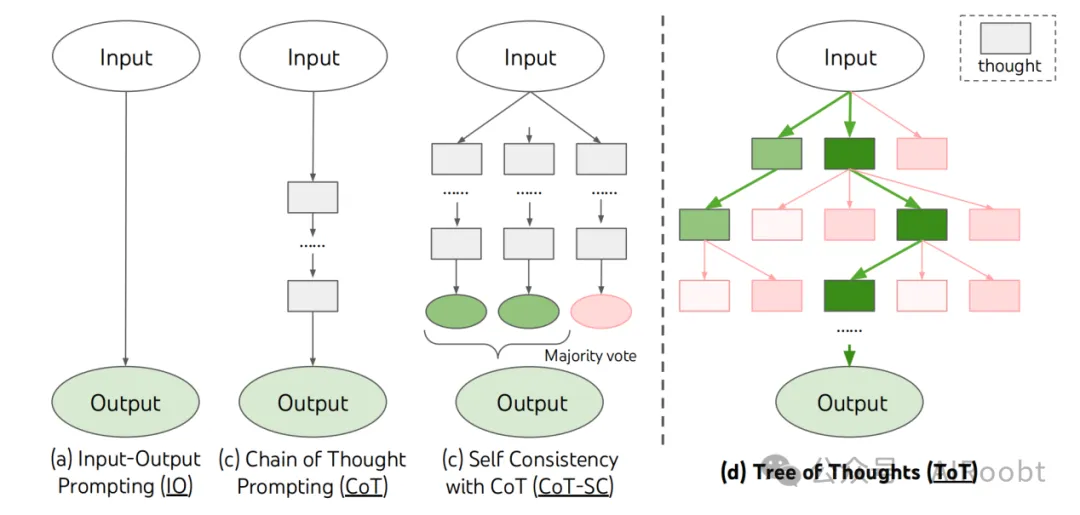
图1：示意图展示了使用大型语言模型进行问题解决的各种方法。每个矩形框代表一个思想，它是一个连贯的语言序列，作为问题解决的中间步骤。有关思想如何生成、评估和搜索的具体示例，请参见图2、图4和图6。

在实证上，我们提出了三种新问题，这些问题即使使用最先进的语言模型GPT-4也会挑战现有的LM推理方法：24点游戏、创意写作和填字游戏。这些任务需要演绎、数学、常识、词汇推理能力，以及一种系统规划或搜索的方法。我们证明了ToT在所有三项任务上都取得了优异的结果，因为它足够通用和灵活，能够支持不同层次的思想，不同的生成和评估思想的方式，以及适应不同问题性质的不同搜索算法。我们还通过系统性消融分析了这些选择如何影响模型性能，并讨论了更好地训练和使用LMs的未来方向。

2.背景

我们首先形式化一些使用大型语言模型进行问题解决的现有方法，这些方法启发了我们的方法，并将在后文进行比较。我们用 p_θ 表示一个带有参数 θ 的预训练语言模型，用小写字母 x, y, z, s, ... 表示一个语言序列，即 x = (x[1], ..., x[n])，其中每个 x[i] 是一个令牌，因此 p_θ(x) = ∏_i=1ⁿ p_θ(x[i]|x[1...i])。我们用大写字母 S, ...表示一个语言序列的集合。

输入-输出（IO）提示是将问题输入 x 转换为输出 y 的最常见方法： y~p_θ(y|prompt_IO(x))，其中 prompt_IO(x) 将输入 x 包装成任务指令和/或少量的输入-输出示例。为了简单起见，我们将 p_θ^prompt(output | input) = p_θ(output | prompt(input))，这样IO提示可以形式化为 y~ p_θ^IO(y|x)。

链式思维（CoT）提示被提出用于解决输入 x 到输出 y 的映射非平凡的情况（例如，当 x 是一个数学问题而 y 是最终的数值答案时）。关键思想是引入一系列思想 z₁, ..., z_n 来连接 x 和 y，其中每个 z_i 是一个连贯的语言序列，作为问题解决的有意义的中间步骤（例如，z_i 可能是数学问答中的中间方程）。为了使用CoT解决问题，每个思想 z_i ~ p^CoT_θ(z_i| x, z_{1 ... i-}1) 依次被采样，然后输出 y ~p^CoT_θ(y|x, z_{1 ... n})。在实际中，[z_{1 ... n}, y] ~ p^CoT_θ(z_{1 ... n}, y|x) 被作为一个连续的语言序列采样，思想的分解（例如每个 z_i 是一个短语、一句话还是一段话）是模糊的。

自一致链式思维（CoT-SC）是一种集成方法，它采样 k 个独立同分布的思想链：[z⁽ⁱ⁾_{1 ... n}, y⁽ⁱ⁾] ~ p^CoT_θ(z_{1 ... n}, y|x) (i = 1 ... k)，然后返回最频繁的输出：arg max_y {i | y⁽ⁱ⁾ = y}。CoT-SC改进了CoT，因为同一问题通常有不同的思维过程（例如证明同一理论的不同方法），通过探索更丰富的思想集可以使输出决策更为准确。然而，在每个链中没有对不同思想步骤的局部探索，并且“最频繁”启发法仅在输出空间有限（例如多选问答）时适用。

3. 思维树：利用LM进行深思熟虑的解决问题

一个真正的问题解决过程涉及重复使用现有信息进行探索，从而揭示更多信息，直到最终发现解决方案。—— Newell等人

关于人类问题解决的研究表明，人们在组合问题空间中进行搜索——一个树状结构，其中节点代表部分解决方案，分支对应修改它们的操作。选择哪个分支由启发式方法决定，这些方法有助于导航问题空间并指导问题解决者走向解决方案。这种观点突显了现有使用LMs解决一般问题的方法的两个主要缺点：1）在局部，他们没有在思想过程的不同延续中进行探索——树的分支。2）在全局，他们没有结合任何类型的规划、前瞻或回溯来帮助评估这些不同的选项——这种启发式指导的搜索似乎是人类问题解决的特征。

为了解决这些缺点，我们引入了思维树（Tree of Thoughts，ToT），一种允许LMs在思想路径上进行多路径探索的范式。ToT将任何问题框架化为树上的搜索，其中每个节点是一个状态 s = [x, z_1···i]，表示带有输入和迄今为止的思想序列的部分解决方案。ToT的具体实现涉及回答四个问题：

1. 如何将中间过程分解为思想步骤；2. 如何从每个状态生成潜在思想；3. 如何启发式地评估状态；4. 使用哪种搜索算法。

1. 思维分解。虽然CoT在没有明确分解的情况下连贯地采样思维，ToT利用问题属性设计并分解中间思维步骤。如表1所示，根据不同问题，思维可以是几个单词（填字游戏），一个方程式（24点游戏），或整段写作计划（创意写作）。一般而言，思维应该足够“小”，以便LMs能够生成有前途且多样的样本（例如，生成整本书通常太“大”而不连贯），但也要足够“大”，以便LMs能够评估其解决问题的前景（例如，生成一个令牌通常太“小”而无法评估）。

2. 思维生成器 G(p_θ, s, k)。给定树状态 s = [x, z_1···i]，我们考虑两种策略来生成下一个思维步骤的 k 个候选项：

3. 状态评估器 V (p_θ, S)。给定不同状态的前沿，状态评估器评估它们在解决问题方面的进展，作为搜索算法确定哪些状态继续探索以及顺序的启发式方法。虽然启发式方法是解决搜索问题的标准方法，但它们通常是编程的（例如DeepBlue）或学习的（例如AlphaGo）。我们提出了第三种替代方案，通过使用LM对状态进行深思熟虑的推理。当适用时，这种深思熟虑的启发式方法比编程规则更灵活，比学习模型更高效。类似于思想生成器，我们考虑两种策略来独立或共同评估状态：

对于这两种策略，我们可以多次提示LM以汇总值或投票结果，以时间/资源/成本换取更真实/稳健的启发式。

4. 搜索算法。最后，在ToT框架内，可以根据树结构使用不同的搜索算法。我们探索了两种相对简单的搜索算法，并将更高级的算法（例如A，MCTS）留待未来工作：

从概念上讲，ToT作为使用LMs进行一般问题解决的方法有几个好处：（1）通用性。IO，CoT，CoT-SC和自我改进可以看作ToT的特例（即有限深度和广度的树；图1）。（2）模块化。基础LM以及思想的分解、生成、评估和搜索过程都可以独立变化。（3）适应性。可以适应不同的问题属性、LM能力和资源限制。（4）便利性。不需要额外的训练，只需一个预训练的LM即可。下一节将展示这些概念上的好处如何转化为在不同问题上强大的实证性能。

4.实验

我们提出了三个任务，即使使用最新的语言模型GPT-4 [23]，采用标准的输入输出提示或思维链（CoT）提示也很难完成。我们展示了在思维树（ToT）中进行有目的的搜索如何产生更好的结果，更重要的是，展示了使用语言模型解决需要搜索或规划的问题的新颖而有前途的方法。除非另有说明，我们使用具有0.7采样温度的GPT-4的Chat Completion模式进行实验。

4.1 24点游戏

24点游戏是一个数学推理挑战，目标是使用4个数字和基本的算术运算（加减乘除）得到24。例如，给定输入“4 9 10 13”，一个解决方案输出可以是“(10 - 4) (13 - 9) = 24”。

任务设置：我们从4nums.com获取数据，该网站有1362个按人类解决时间从易到难排序的游戏，并使用索引为901-1000的相对较难的游戏子集进行测试。对于每个任务，如果输出是一个等于24的有效方程，并且使用输入数字各一次，我们就认为任务成功。我们报告100个游戏的成功率作为指标。

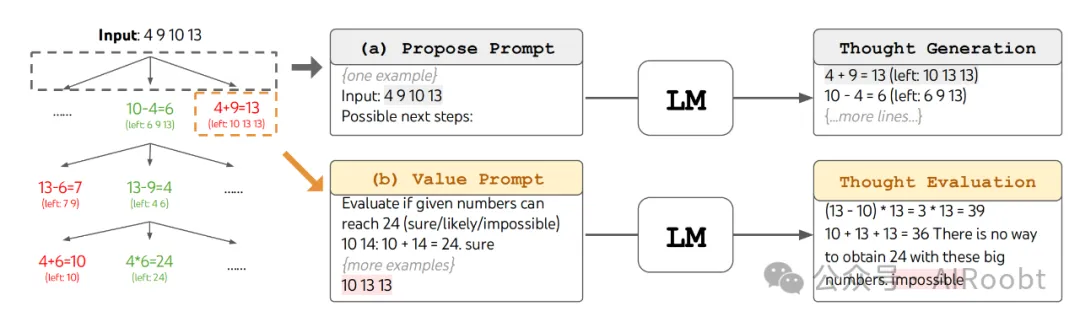
图2：在24点游戏中的思维树（ToT）。语言模型用于(a)思维生成和(b)评估。

（注释：在24点游戏中应用思维树（ToT）方法来生成和评估语言模型（LM）的思维。这种方法分为两个主要步骤：（a）思维生成和（b）思维评估。以下是详细的工作原理讲解：

1. 输入和初始状态

- 输入是一组数字，例如“4 9 10 13”。

- 目标是通过基本的算术运算（加、减、乘、除）将这些数字组合成24。

2. 思维生成（Propose Prompt）

- 步骤 (a): 生成下一步的可能操作。

- 语言模型（LM）根据输入提示生成可能的下一步操作。输入提示（Propose Prompt）包含一个示例输入“4 9 10 13”，并要求模型生成可能的下一步操作。

- 模型可能生成的操作包括例如“4 + 9 = 13（剩下：10 13 13）”和“10 - 4 = 6（剩下：6 9 13）”。

3. 思维评估（Value Prompt）

- 步骤 (b): 评估生成的操作的有效性。

- 语言模型（LM）根据评估提示（Value Prompt）对生成的操作进行评估。评估提示要求模型判断给定的数字是否能达到24，结果分为“确定（sure）”、“可能（likely）”或“不可能（impossible）”。

- 例如，模型可能评估“10 14：10 + 14 = 24”为“确定（sure）”，并给出进一步的操作建议。

4. 思维树的构建

- 图的左侧展示了一个思维树的分支结构，每个节点表示一个操作及其剩余数字。

- 例如，起始节点是“4 9 10 13”，通过“10 - 4 = 6（剩下：6 9 13）”和“4 + 9 = 13（剩下：10 13 13）”生成了两个子节点。

- 每个子节点继续生成进一步的操作，形成分支，例如“13 - 6 = 7（剩下：7 9）”和“13 - 9 = 4（剩下：4 6）”。

5. 操作的具体评估

- 图的右侧展示了模型在生成和评估思维过程中的具体操作。

- 思维生成：模型生成具体操作如“4 + 9 = 13（剩下：10 13 13）”和“10 - 4 = 6（剩下：6 9 13）”。

- 思维评估：模型评估每个生成操作的有效性。例如，模型可能会评估“(13 - 10) * 13 = 39”和“10 + 13 + 13 = 36”为不可能达到24，标记为“不可能（impossible）”。

6. 结果和决策

- 基于模型的生成和评估，最终选择最有可能达到24的操作路径。

- 例如，经过几轮操作和评估后，模型可能选择一条路径如“4 * 6 = 24（剩下：24）”，并确认这是一个成功的操作。

结论

通过这种有目的的搜索和评估，思维树（ToT）方法能够更有效地解决24点游戏等需要多步骤规划和决策的问题。每一步生成和评估的结合，使得模型能够排除不可能的路径，集中资源在最有前途的操作上，提高了问题解决的效率和成功率。）

基线：我们使用具有5个上下文示例的标准输入输出（IO）提示。对于思维链（CoT）提示，我们为每个输入输出对增加了3个中间方程，每个方程操作两个剩余数字。例如，给定输入“4 9 10 13”，思维可能是“13 - 9 = 4（剩下：4 4 10）；10 - 4 = 6（剩下：4 6）；4  6 = 24（剩下：24）”。对于每个游戏，我们抽样100次IO和CoT提示以获得平均性能。我们还考虑了一个CoT自洽基线，它从100个CoT样本中选出多数输出，并在IO样本基础上进行最多10次迭代的迭代精炼方法。在每次迭代中，如果输出不正确，语言模型将根据所有先前的历史生成“反思你的错误并生成改进的答案”。注意，它使用关于方程正确性的真实反馈信号。

ToT设置：为了将24点游戏框架化为ToT，自然地将思维分解为3步，每步一个中间方程。如图2(a)所示，在每个树节点，我们提取剩余数字并提示语言模型提出一些可能的下一步。同样的“建议提示”用于所有3个思维步骤，尽管它只有一个带有4个输入数字的示例。我们在ToT中执行宽度优先搜索（BFS），在每一步我们保留最好的5个候选者。为了在ToT中进行有目的的BFS，如图2(b)所示，我们提示语言模型评估每个思维候选者关于到达24的“确定/可能/不可能”。目的是在少量前瞻试验内促进正确的部分解决方案，并基于“太大/太小”的常识消除不可能的部分解决方案，并保留其余的“可能”。我们为每个思维抽样3次。

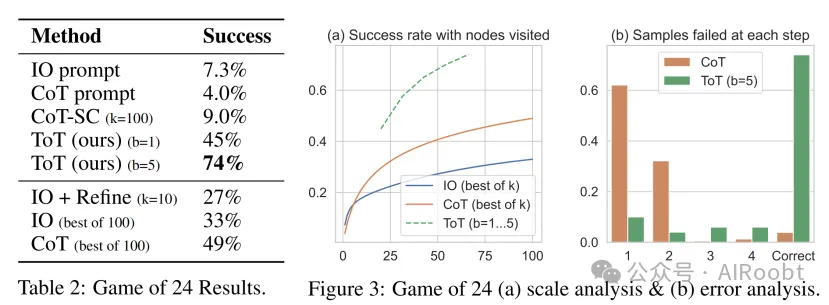
结果：如表2所示，IO、CoT和CoT-SC提示方法在该任务上的表现很差，成功率仅为7.3%、4.0%和9.0%。相比之下，宽度为1的ToT成功率已达到45%，而宽度为5时成功率达到74%。我们还考虑了IO/CoT的Oracle设置，通过使用最好的k个样本（1 ≤ k ≤ 100）计算成功率。为了比较IO/CoT（最佳k样本）与ToT，我们考虑计算在ToT中每个任务访问的树节点数在b = 1 ··· 5范围内，并在图3(a)中绘制5个成功率，将IO/CoT（最佳k样本）视为在bandit中访问k个节点。不出所料，CoT比IO扩展得更好，100个CoT样本中的最佳样本成功率达到49%，但仍远不及在ToT中探索更多节点（b > 1）。

错误分析：图3(b)分解了CoT和ToT样本在任务中的失败步骤，即思维链中的思维（在CoT中）或所有b个思维（在ToT中）无效或不可能达到24。值得注意的是，大约60%的CoT样本在生成第一步或等效的前三个单词（例如“4 + 9”）后已经失败。这凸显了直接从左到右解码的问题。

4.2 创意写作

接下来，我们设计了一个创意写作任务，输入为4个随机句子，输出应为一个连贯的段落，其中4个段落分别以4个输入句子结尾。这样的任务是开放性和探索性的，挑战了创意思维和高层次的规划能力。

任务设置：我们从randomwordgenerator.com上随机抽取句子形成100个输入，每个输入约束没有标准答案。由于我们发现GPT-4大多数情况下能遵循输入约束，我们重点评估段落连贯性，采用两种方式：使用GPT-4零样本提示提供1-10的标量评分，或使用人工判断比较不同方法的输出对。对于前者，我们对每个任务输出抽取5个评分并取平均值，这5个评分通常一致，输出的标准差平均约为0.56。对于后者，我们在盲测中让部分作者比较CoT和ToT生成的段落对的连贯性，段落顺序在100个输入中随机翻转。

基线：考虑到任务的创意性质，IO和CoT提示都是零样本。前者提示语言模型在给定输入约束的情况下直接生成连贯的段落，后者提示语言模型先做一个简短的计划再写段落，即计划作为中间思维步骤。我们为每个任务生成10个IO和CoT样本。我们还考虑了一种迭代精炼方法（ k \leq 5 ），在每个任务的随机IO样本基础上进行迭代，语言模型根据输入约束和最后生成的段落判断段落是否“完美连贯”，如果不是，则生成改进的段落。

ToT设置：我们构建了一个深度为2的ToT（只有1个中间思维步骤）——语言模型首先生成5个计划并投票选出最佳计划（图4），然后基于最佳计划生成5个段落并投票选出最佳段落。这里宽度限制  b = 1 ，每步只保留一个选择。我们在两个步骤都使用一个简单的零样本投票提示（“分析下面的选择，然后总结哪个最有希望完成指令”）抽取5票。

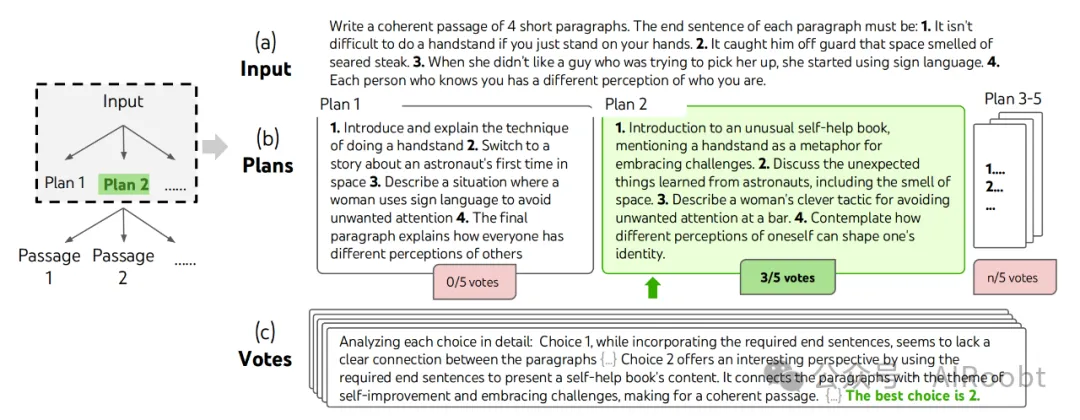
图4：在一个随机选取的创意写作任务中进行有目的搜索的一个步骤。给定输入后，语言模型生成5个不同的计划，然后投票5次决定哪个计划最佳。多数票选出的计划将用于按照相同的生成-投票程序撰写输出段落。

（注释:在一个随机选取的创意写作任务中进行有目的搜索的一个步骤。

(a) 输入 (Input)

- 任务说明：任务是写一个包含4个短段落的连贯段落，每个段落的结尾句子必须是指定的4个句子。

- 这些结尾句子分别是：

1. It isn't difficult to do a handstand if you just stand on your hands.

2. It caught him off guard that space smelled of seared steak.

3. When she didn’t like a guy who was trying to pick her up, she started using sign language.

4. Each person who knows you has a different perception of who you are.

(b) 计划生成 (Plans)

- 步骤 (b)：语言模型根据输入生成多个不同的计划。

- 计划1：

1. 介绍和解释做倒立的技巧

2. 转换到一个关于宇航员第一次进入太空的故事

3. 描述一个女人使用手语避免不必要注意的情况

4. 最后一个段落解释每个人对他人的不同看法

- 得票：0/5票

- 计划2：

1. 介绍一本不寻常的自助书，提到做倒立作为迎接挑战的隐喻

2. 讨论从宇航员身上学到的意外事情，包括太空的气味

3. 描述一个女人在酒吧避免不必要注意的巧妙策略

4. 思考对自己的不同看法如何塑造个人身份

- 得票：3/5票（最终选中）

- 计划3-5：类似于计划1和计划2，但未显示具体内容。

(c) 投票 (Votes)

- 步骤 (c)：评估和投票。

- 分析和评价每个选择：

- 选择1：尽管包含所需的结尾句子，但段落之间缺乏明确的连接。

- 选择2：提供了一个有趣的视角，通过使用所需的结尾句子展示了自助书的内容。它将段落与自我提升和迎接挑战的主题连接起来，形成连贯的段落。

- 最终选择：最佳选择是计划2。

工作原理总结

1. 输入阶段：明确任务要求，即需要生成包含指定结尾句子的连贯段落。

2. 计划生成阶段：语言模型生成多个计划，每个计划都尝试符合输入要求并形成一个完整的故事。

3. 投票和评估阶段：对生成的计划进行评估，通过投票选择最符合任务要求的计划。

4. 最终输出：选中的计划用于撰写最终的输出段落。

这种有目的的搜索方法通过生成多个候选计划并进行评估和投票，有效提高了输出内容的连贯性和质量。）

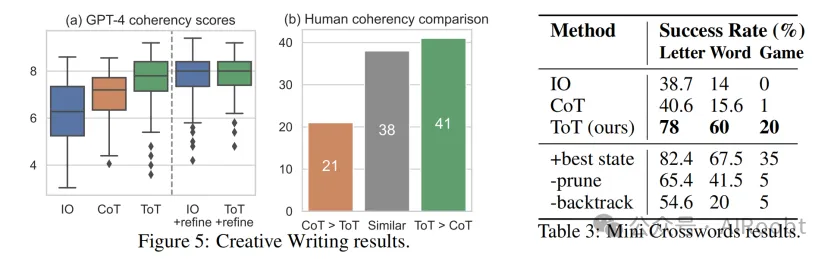
结果：图5(a)显示了100个任务的平均GPT-4评分，其中ToT（7.56）被认为生成的段落比IO（6.19）和CoT（6.93）更连贯。尽管这种自动评分可能有噪音，图5(b)通过展示人工偏好ToT而非CoT的41对段落（在100对中），而仅偏好CoT的21对（另有38对被认为“同样连贯”），确认了这一发现。最后，迭代精炼在这个自然语言任务中更有效，IO连贯性评分从6.19提高到7.67，ToT连贯性评分从7.56提高到7.91。我们认为这可以被视为ToT框架中思维生成的第三种方法，其中新思维可以通过精炼旧思维而不是独立同分布或顺序生成。

4.3 迷你填字游戏

在24点游戏和创意写作中，ToT相对较浅——最多需要3个思维步骤才能达到最终输出。在这里，我们探索5×5迷你填字游戏作为一个涉及自然语言的更难的搜索问题。目标不仅仅是解决任务，因为更一般的填字游戏可以通过利用大规模检索而不是语言模型的专业NLP管道轻松解决[34]。相反，我们旨在探索语言模型作为一个通用问题解决者的极限，它探索自己的思维并用有目的的推理作为启发式引导自己的探索。

任务设置：我们从GooBix抓取数据，其中包含156个5×5迷你填字游戏。由于我们观察到相邻的游戏包含类似的线索，我们使用索引为1、6、···、91、96的20个游戏进行测试，索引为136、141、146、151、156的游戏进行提示。对于每个任务，输入描述了5个水平线索和5个垂直线索，输出应为一个5×5 = 25个字母的棋盘以解决填字游戏。对于评估，我们考虑三个层次的成功：正确字母的部分（每局25个字母）、单词（每局10个单词）和游戏。

基线：我们在IO提示中提供5个输入输出对的示例，在CoT提示中还包括按顺序的中间单词  h1..5  和  v1..5 。我们为每个提示运行10个样本并平均结果。

ToT设置：我们利用深度优先搜索（算法2），不断探索最有前途的后续单词线索，直到状态不再有前途，然后回溯到父状态以探索其他思维。为了使搜索变得可行，后续思维被限制为不改变任何已填充的单词或字母，以便ToT最多有10个中间步骤。对于思维生成，在每个状态下我们将所有现有的思维（例如“h2.motor；h1.tasks”对于图6(a)中的状态）翻译成剩余线索的字母约束（例如“v1.To heap: tm;...”），并提示5次建议提示以提出下一个单词的填充位置和内容。重要的是，我们还提示语言模型对不同的思维给出置信度，并在提案中聚合这些置信度以获得下一步探索的排序思维列表（图6(a)）。对于状态评估，我们类似地将每个状态翻译成剩余线索的字母约束，然后评估每个线索在给定约束下是否可填充。如果任何剩余线索被认为“不可填”（例如“v1.To heap: tm s”），则该状态的子树探索被修剪，DFS回溯到其父状态以探索下一个有前途的思维。我们将DFS搜索步骤限制为100步，并简单地将最深探索的状态（如果有多个则为第一个）渲染为最终输出。

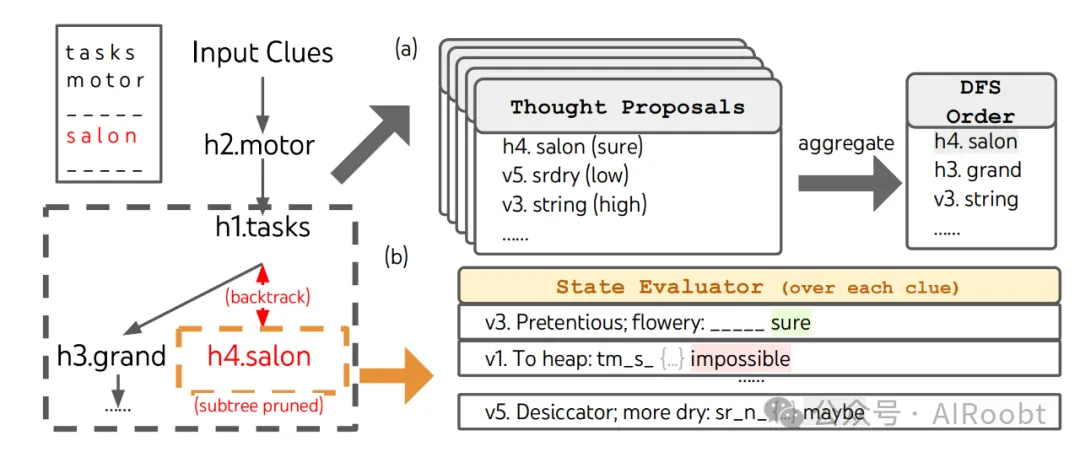
图6：在迷你填字游戏中，(a) 思维如何在深度优先搜索（DFS）中提出并在优先队列中聚合，(b) 如何基于填入每个剩余单词线索的可能性评估状态，如果任何剩余线索被语言模型认为不可填，则进行修剪。然后DFS回溯到父状态，并探索下一个有前途的线索思维。

（注释：在迷你填字游戏中应用深度优先搜索（DFS）时思维的提出和评估过程。

(a) 思维提出 (Thought Proposals)

- 输入线索 (Input Clues)：如图左上角所示，输入线索包括一组需要填字的单词提示。已填字母如“tasks”、“motor”和“salon”。

- 思维提出：

- 语言模型根据现有的输入线索提出多个可能的填字方案。例如，“h4.salon（确定）”、“v5.srdry（低）”和“v3.string（高）”。

- 这些思维被放入一个优先队列中进行聚合，根据其可能性和优先级排序。

(b) 状态评估 (State Evaluation)

- DFS 顺序 (DFS Order)：图右上角展示了根据优先级排序后的DFS顺序，例如“h4.salon”、“h3.grand”和“v3.string”。

- 状态评估：

- 每个状态的评估基于填入每个剩余单词线索的可能性进行。

- 状态评估器 (State Evaluator) 会对每个线索进行评估。例如：

- v3. Pretentious; flowery: _____（确定）

- v1. To heap: tm_s_（不可能）

- v5. Desiccator; more dry: sr_n_（可能）

深度优先搜索 (DFS) 和修剪 (Pruning)

- DFS 执行过程：

- DFS首先探索优先队列中的最高优先级思维，例如“h4.salon”。

- 如果某个状态的任何剩余线索被评估为“不可能”，则该状态的子树会被修剪（subtree pruned），如图中红色标注的“h4.salon”。

- 修剪后，DFS会回溯到父状态，继续探索下一个有前途的思维，例如从“h4.salon”回溯到“h1.tasks”，再探索“h3.grand”。

总结

在迷你填字游戏中如何通过深度优先搜索（DFS）进行思维提出和状态评估：

1. 思维提出：基于输入线索，语言模型生成多个可能的填字方案，并将其按优先级排序。

2. 状态评估：每个状态根据填入每个剩余单词线索的可能性进行评估。如果评估结果为“不可能”，则该状态会被修剪。

3. 深度优先搜索：通过DFS探索最有前途的思维，遇到不可能的状态时回溯并继续探索其他可能的思维。

这种方法能够有效地利用语言模型的能力，在复杂的填字游戏中进行有目的的搜索和评估，提高问题解决的效率和成功率。）

结果：如表3所示，IO和CoT提示方法在单词级成功率不到16%的情况下表现不佳，而ToT显著改善了所有指标，单词级成功率达到60%，解决了20个游戏中的4个。这样的改进并不令人意外，因为IO和CoT缺乏尝试不同线索、修改决策或回溯的机制。

Oracle和消融研究：在每个任务中输出Oracle最佳DFS状态（而不是启发式确定的最佳状态）时，ToT的性能甚至更高，实际上解决了7/20个游戏（表3，“+最佳状态”），这表明我们的简单输出启发式可以得到改进。有趣的是，有时当填字游戏实际上解决了，状态评估器仍可能认为某些单词“不可填”并修剪——可能是因为5×5填字游戏设计上有一些稀有或过时的词汇，GPT-4无法识别。由于状态评估作为修剪启发式是不完美的，我们还探索了消融修剪，发现性能总体较差（表3，“-修剪”）。然而，它实际上可以找到4/20个游戏的正确解决方案（尽管仅输出1个通过启发式），其中3个是ToT+修剪在100步内无法解决的游戏。因此，改进DFS修剪的启发式对于解决此类问题至关重要。最后，我们通过运行一个消融实验确认了回溯的重要性，在该实验中最多允许填充20步的最有前途线索，允许覆盖。这类似于宽度限制为  b = 1  的“贪心”BFS搜索，单词级成功率仅为20%（表3，“-回溯”）。

5. 相关工作

规划和决策：智能规划和决策对实现预定目标至关重要。由于语言模型（LMs）在大量世界知识和人类示例上训练，已知它们已经吸收了丰富的常识，使得根据问题设置和环境状态提出合理计划成为可能[12, 42, 37, 13, 35, 41, 40]。我们提出的思维树（ToT）方法通过在每一步问题解决过程中同时考虑多个潜在可行的计划，并继续最有前途的计划，扩展了现有的规划形式。思维采样与价值反馈的结合有机地整合了规划和决策机制，能够在解决方案树中进行有效搜索。另一方面，传统的决策过程通常需要训练专门的奖励和策略模型，如强化学习中的CHAI[33]，而我们使用语言模型本身提供决策所需的价值评估。RAP[9]是一个将语言模型推理视为其内部世界模型规划的并发工作，并提出了一种类似ToT的MCTS方法。然而，其任务比我们的简单，并且其框架缺乏整合不同树搜索算法的模块化。

自我反思：使用大型语言模型（LLMs）评估其自身预测的可行性在问题解决中变得越来越重要。[28, 20, 24]引入了“自我反思”机制，在此机制中，语言模型为其生成的候选项提供反馈。[4]通过注入语言模型基于其代码执行结果生成的反馈消息，提高了语言模型代码生成的准确性。同样地，[17]也在计算机操作任务中引入了对操作和状态的“批评”或审查步骤，决定下一步采取的行动。另一项与我们工作非常相关的近期研究是“自我评估引导解码”[39]。与我们的方法类似，自我评估解码也遵循树搜索过程，叶节点从随机束搜索解码中抽样，然后由语言模型本身使用精心准备的自我评估提示进行评估。然而，他们的方法使用PAL形式[8]，将思维表示为代码，这使得处理如本论文中考虑的创意写作等具有挑战性的任务变得困难。因此，我们的思维树方法更加通用，能够处理GPT-4在标准提示下仅能达到非常低准确率的挑战性任务。

程序引导的语言模型生成：我们的提议也与最近的进展有关，这些进展通过系统程序[14, 44, 6, 43]或符号程序引导来组织语言模型的行为。例如，Schlag等人[27]将语言模型嵌入到算法搜索过程中，帮助逐步解决问题，如回答问题，其中搜索树由可能提供答案的相关段落扩展。然而，该方法与我们的方法不同，因为树通过抽样外部段落而非语言模型自身的思维进行扩展，并且没有反思或投票步骤。另一种方法，LLM+P[18]，更进一步，将实际的规划过程委托给传统的规划者。

经典搜索方法：最后但同样重要的是，我们的方法可以被视为经典搜索方法在问题解决中的现代演绎。例如，它可以被视为一种启发式搜索算法，如A[10]，在每个搜索节点的启发式由语言模型的自我评估提供。从这个角度来看，我们的方法也与NeuroLogic Aesque解码[19]相关，后者受A搜索启发，引入了前瞻启发式，对于提高束搜索或top-k抽样解码的语言模型来说是高效的。然而，该方法限制于句子生成任务，而我们的框架设计用于复杂的、多步骤的问题解决，由价值反馈进行保护。

6.讨论

限制和未来方向：像ToT这样的有目的搜索可能对于GPT-4已经擅长的许多现有任务（见附录B.1）并不必要，作为初步工作，本研究仅探索了三个相对简单的挑战GPT-4的任务（见附录B.2中的一些GPT-3.5实验结果），并呼吁将更好的搜索和规划能力整合到语言模型中。然而，当我们开始将语言模型部署到更多现实世界的决策应用中（如编码、数据分析、机器人技术等），更复杂的任务可能会出现，并为研究这些问题提供新机会。此外，为了提高任务性能，像ToT这样的搜索方法需要比采样方法更多的资源（如GPT-4 API费用），但ToT的模块化灵活性允许用户定制这种性能-成本权衡，并且正在进行的开源努力[32]应该会在不久的将来减少这些成本。更多关于成本和效率的详细信息见附录B.3。最后，这项工作侧重于使用现成的语言模型，并且使用ToT风格的高层反事实决策进行语言模型微调（如权衡下一段的潜在选择，而不是预测下一个标记）可能会增强语言模型的问题解决能力。

结论：语言模型的联想“系统1”可以通过基于搜索问题解决路径树的“系统2”得到有益的增强。思维树框架提供了一种将关于问题解决的经典见解转化为现代语言模型可操作方法的途径。同时，语言模型解决了这些经典方法的弱点，提供了一种解决难以形式化的复杂问题（如创意写作）的途径。我们认为，语言模型与经典AI方法的交叉是一个令人兴奋的方向。

更广泛的影响：ToT是一个使语言模型能够更自主和智能地做出决策和解决问题的框架。虽然当前任务仅限于推理和搜索问题，未来涉及与外部环境或人类互动的应用可能会带来潜在危险，如促进语言模型的有害使用。另一方面，ToT也提高了模型决策的可解释性和人类对齐的机会，因为结果表示是可读的高层语言推理，而不是隐含的低层标记值。

Yao S, Yu D, Zhao J, et al. Tree of thoughts: Deliberate problem solving with large language models[J]. Advances in Neural Information Processing Systems, 2024, 36.

1 Princeton University

2 Google DeepMind

本文转载自公众号AIRoobt ，作者：AIRoobt

原文链接：​​​​https://mp.weixin.qq.com/s/DgtXskiQmrdmkYAg5oNXbQ​​​