你知道神经网络是怎么运作的吗？神经网络内部原理解析 原创

“ 神经网络就是一个具有输入和输出的黑盒”

神经网络模型就是模仿人类大脑神经元传递的过程，从使用者的角度来说，神经网络就是一个具有输入和输出的黑盒模型。

简化模型如下图：

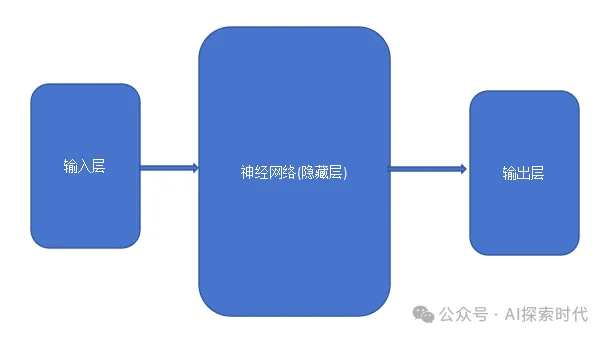
只需要设定特定的输入和输出格式，隐藏层可以根据不同的任务需求进行实现。

01、神经网络模型

神经网络主要由神经元构成，然后会根据任务复杂度，设计一个到多个网络层，网络层数越多，处理的问题越复杂。

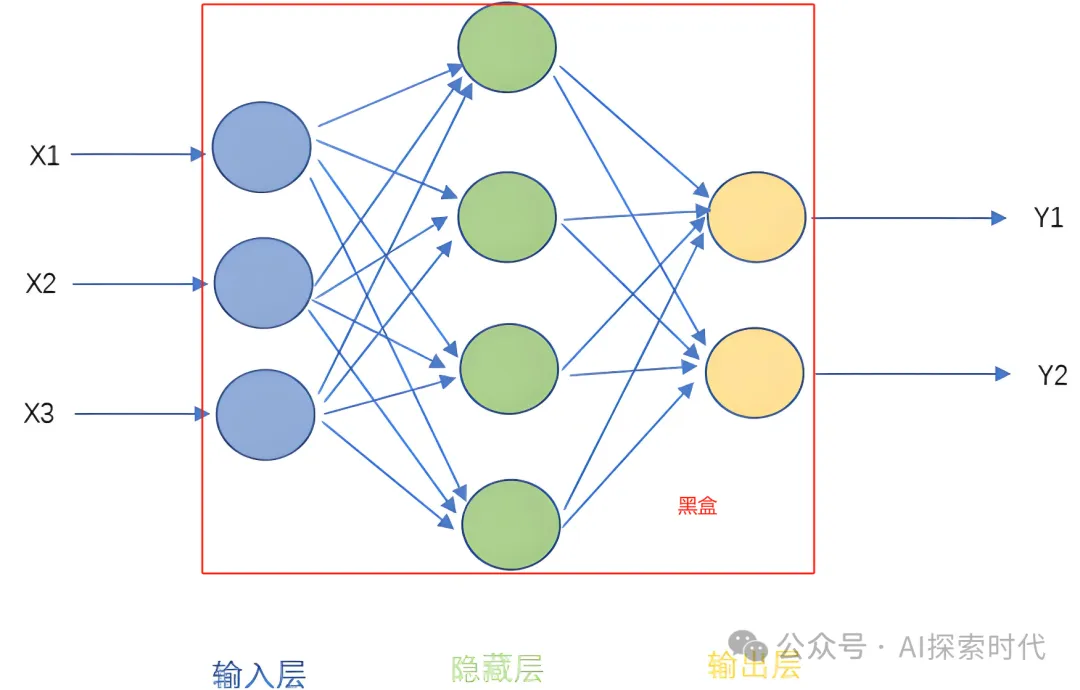
如下图所示，就是一个简单的神经网络模型图，具有输入层，输出层和隐藏层，隐藏层并不一定就一层，也可能由多层网络组成，每一层又由多个神经元组成。

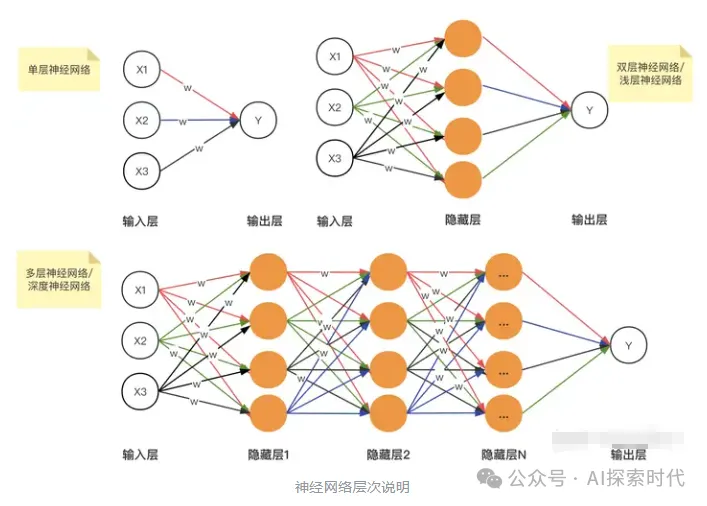
神经网络可以分为：输入层、隐藏层、输出层，其中隐藏层数量决定模型网络复杂度

输入层是神经网络的第一层，其作用是接收输入数据，并将其传递到下一层。

隐藏层是位于输入层和输出层之间的一层或多层。其作用是将输入数据转换为更高层次的特征表示，神经网络的核心处理模块就在隐藏层。

输出层是神经网络的最后一层，其作用是将神经网络对输入数据的处理结果输出。

输入层

输入层是神经网络的第一层，也是唯一与外界交互的一层，它的作用就是从外界获取数据，并输入到它的下一层，它的下一层可以是隐藏层也可以是输出层。

在神经网络中，输入层是需要从外部获取数据，而不是由训练得到的数据；因此，在神经网络的设计中，输入层需要根据不同的数据特征进行适当的调整和泛化。

比如在图像处理的神经网络中，需要考虑图片的尺寸，颜色空间等；而在自然语言处理(NLP)中，又需要考虑分词，词汇表等。

输入层的神经元数量一般由输入的数据特征来确定，比如图片处理任务中，每一个像素点就是一个神经元。

因此，输入层作为神经网络的第一层，它的作用就是把输入数据(文字，图片，视频等一切数据)，转化为神经网络可以处理的格式。

所以，在设计输入层时，要考虑输入数据的格式及各种预处理，并且要具有适当的泛化能力，比如某一天需要增加某些数据格式等，并且根据不同的任务类型可以进行适当的调整。

输入层就类似于一个适配器或转化器，把人类的数据格式适配到神经网络中。

隐藏层

隐藏层是位于输入层与输出层之间的一层或多层，隐藏层是神经网络的核心处理模块，它可以把输入层的数据转换为更高层次的特征表示；并且，每个隐藏层的神经元数量和连接方式都不相同，这取决于具体的神经网络架构。

比如，卷积网络的隐藏层主要有卷积层，池化层和线性层。

隐藏层的好坏和架构，直接决定着这个神经网络的功能与性能，以及训练的成本等问题。隐藏层的神经元越多，网络层数越多，那么它的表示能力越强，处理的问题也就更复杂。

因此，隐藏层的设计也需要根据不同的任务类型进行适当的泛化和调整，并且设计一个良好的隐藏层也需要丰富的理论基础以及实践经验。

随着神经网络的发展，隐藏层会变得越来越多，越来越复杂；也可能会出现更加新颖和强大的架构。

输出层

输出层是神经网络模型中的最后一层，其作用是输出神经网络的处理结果，严格来说是隐藏层的处理结果；输出层一般只有一个神经元，其值就是神经网络的处理结果。

在训练的过程中，输出层的输出结果需要使用损失函数计算损失差，而训练的目的就是不断的减少损失差。

输出层同样也需要根据不同的任务类型，进行适当的泛化和调整设计，这样才能满足更加复杂的输出任务。

总结

根据不同的任务，神经网络也分为不同的类型，比如分类任务，文本处理任务，图片处理任务等。

根据不同的网络架构也有不同的实现方式，比如全链接层就需要所有神经元参与计算。

在由多层网络组成的隐藏层中，每一层的输入都是上层的输出，每一层的输出就是下一层的输入。

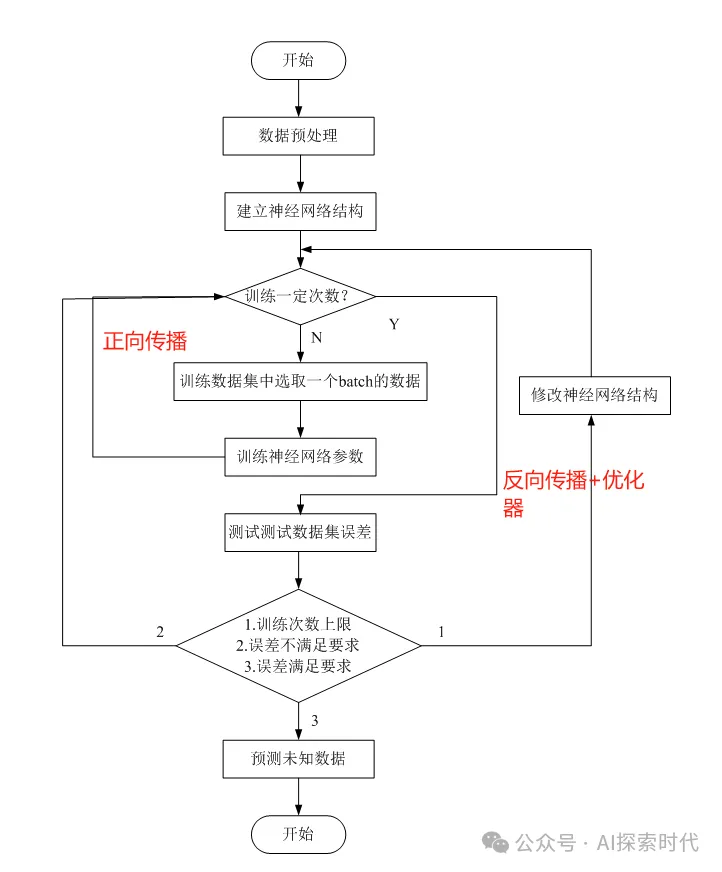
简单来说，神经网络就由其三大组件(输入层，隐藏层和输出层)组成，每一层根据不同的任务都会有不同的实现，重要的就是其泛化和扩展的能力。

最后，经过损失函数计算损失差，并通过反向传播的方式，使用优化器优化网络各层的参数，最后使模型达到最优。

02、神经元的原理

神经元是神经网络的最小组成单位，每一层神经网络都至少由一个神经元到多个神经元组成。

如下图所示就是一个神经元的计算模型图：

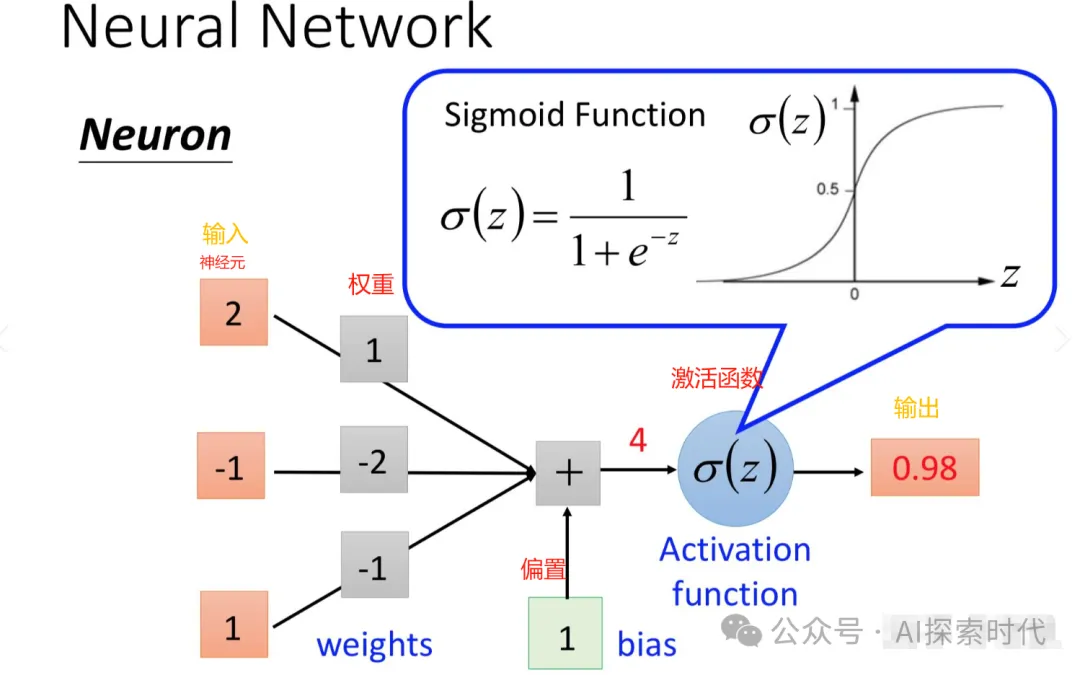
图中左边橙色部分作为输入，其值来源于上层网络神经元的输出，每一个输入就代表着上层的一个神经元。

这时可能有人会奇怪，一个神经元的输出是固定值，那么如果下层网络中有多个神经元，每个神经元都接受同样的输入，这样还有什么意义？

这个就是权重的作用了，由多个上层神经元作为输入，每个神经元都会有一个权重，不同的权重就会有不同的结果。

最简单的神经元计算公式如下：

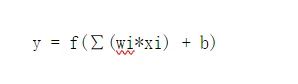
就是把每个神经元的输入Xi乘以权重Wi累加之后，在加上当前神经元的偏置值bias。

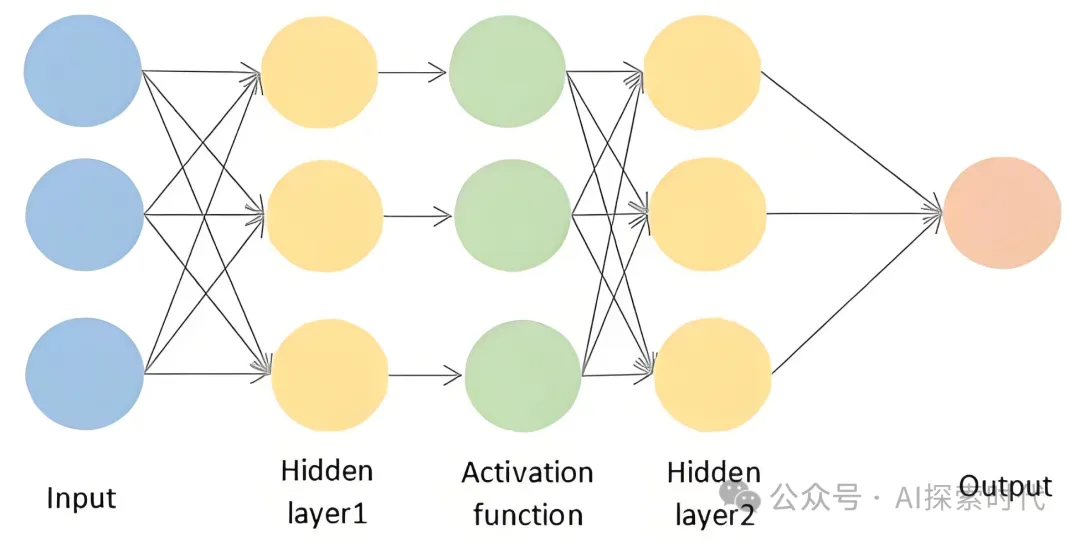
激活函数

输入数据经过神经元计算之后，并不是直接进行输出，而是需要激活函数进行计算，根据阈值判断输出结果。公式如上图蓝色框所示。

神经元计算结果z需要作为激活函数的输入，然后经过计算产生输出。

比如，当激活函数的结果大于0.5时，输入正确；小于0.5时输出错误。

这就是激活函数的作用。

公式如下，紫色部分作为输入，w表示权重；绿色部分是神经元的实现算法，最后经过红色部分激活函数产生输出y。

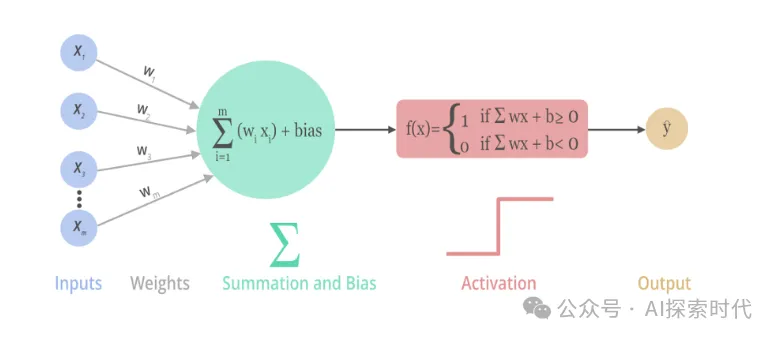
如下所示，是M-P神经元模型图，其也是神经元的经典模型

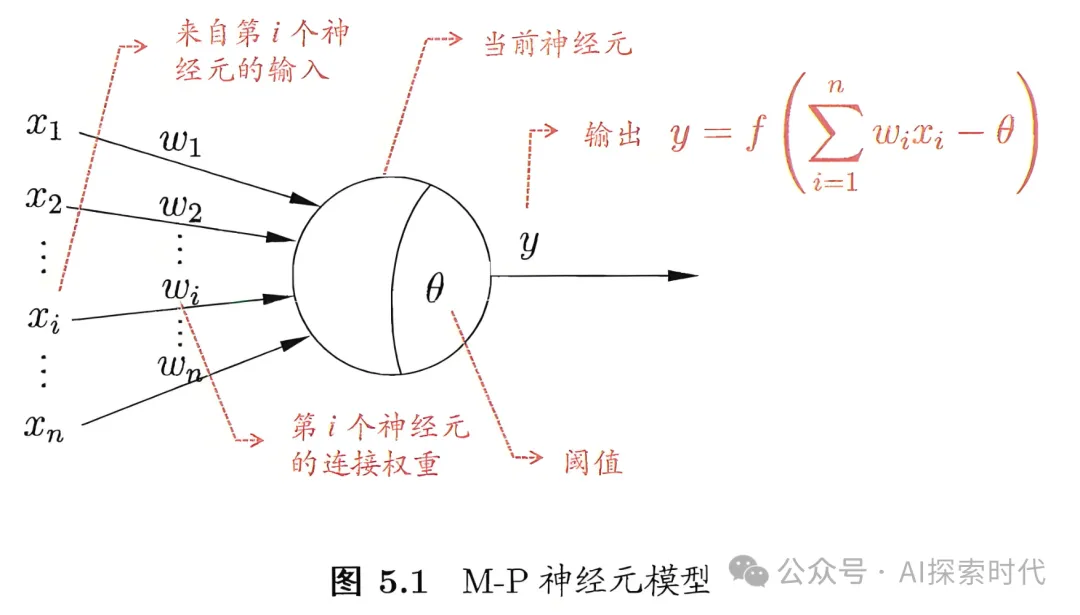
本文转载自公众号AI探索时代 作者：DFires

原文链接：​​https://mp.weixin.qq.com/s/Ine8ULkG_Wd2SaNI2tQgJg​​