向量——人工智能技术的基石结构 原创

“ 向量，人工智能技术的基础结构。”

了解过人工智能技术的人应该都听说过向量，向量可以说是人工智能的数据基础。

那么什么是向量，为什么选择向量呢？

什么是向量？

向量其实来源于数学，是几何学中的一种，指的是具有大小和方向的量，一般用有向线段表示，在中学数学中向量是绝对值为1的，具有方向的量。

而用代数的方式表示向量，则是一个有序数组，包含n个元素(n在多维空间中)。

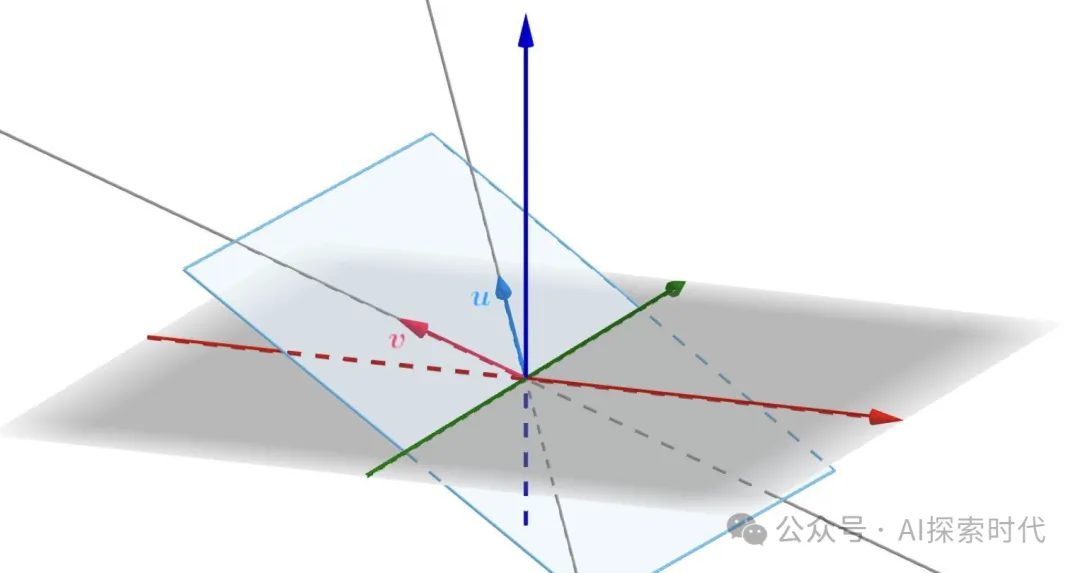
但向量并不只是数学独有的东西，在物理学，工程学中都有使用。从数学的角度来说，向量可以进行数学运算，并且具有一定的数学性质，比如平移不变，方向唯一等。

向量有几个特性，维数是其包含的元素数量，例如：v=[1,2,3]是一个三维向量。其次就是大小和方向，向量的大小可以通过欧几里得范数计算；而其方向是由各分量的比率决定。

向量在人工智能领域的应用

说到人工智能，向量就是一个绕不过去的坎。

我们知道，数学是一切学科的基础，而计算机技术也是建立在数学的理论之上，而人工智能技术作为目前计算机，数学等多学科集大成的技术，当然也离不开数学的理论基础。

而向量就是目前人工智能领域，最基础的数据结构。

首先，人工智能技术中数据的表示采用的是向量，比如文本——词嵌入(Word2Vec,  GloVe)，图片——卷积神经网络提取图像特征，使用向量表示，音频——音频信号通过傅立叶变换等方法转化为频谱。

其次，在机器学习等模型中，输入与输出采用的都是向量的格式；在大模型的训练过程中，第一件事就是数据处理，然后转化为向量形式，只有这样才能被模型所处理。

再者，向量相似性计算在推荐系统，信息检索等领域被广泛应用，比如常见的向量数据库。

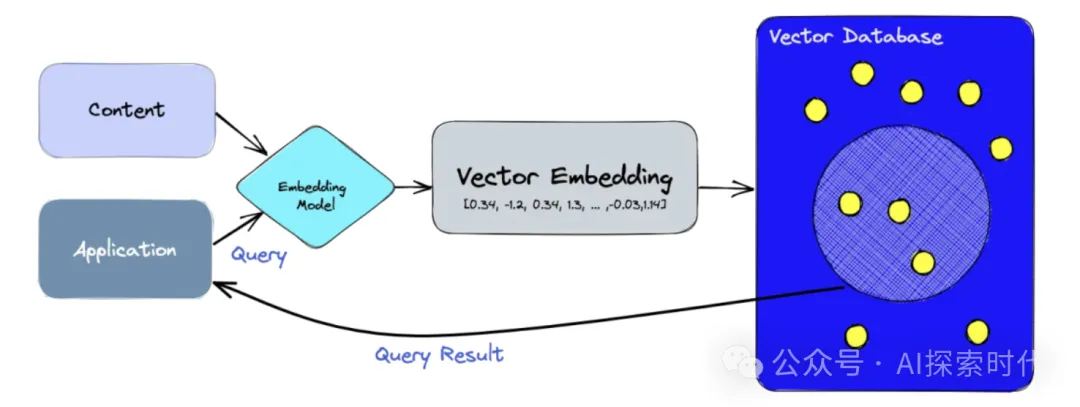
向量数据库是一种能够进行语义查询等数据库，而不是普通的关系型数据库只能进行字符匹配，包括精确匹配和模糊匹配。

而具体的计算方式，如余弦相似度，欧式距离，曼哈顿距离等都是采用的向量形式。

在人工智能领域中，对高纬向量进行降维计算，以及神经网络模型中，隐藏层的数据处理都离不开向量(张量)计算。

向量是人工智能中基本且重要的数据表示形式。它在数据表示、模型输入输出、相似性计算、特征提取等方面有广泛应用，支持了人工智能技术的发展和应用。通过向量化操作，复杂的数据处理和分析变得更加高效和统一。

虽然说，在现有的人工智能理论中，并不能完全明白为什么大规模的参数通过向量运算可以得到近似“智能”的结果，但这并不耽误人工智能技术的演化过程。

本文转载自公众号AI探索时代 作者：DFires

原文链接：​​https://mp.weixin.qq.com/s/Jyf1gEVVgxEmMwk4j5yRYw​​