完全在频域学习的时序预测模块，提升各类SOTA模型效果

今天给大家介绍一篇浙大、中南、南洋理工、上交、北大等多所高校联合提出的一种时间序列预测建模方法，针对目前时序预测直接预测方法没有考虑到预测各个时间步关系的问题，提出了在频域中进行预测的方法，可适配到各类时序SOTA模型中，取得了长短周期时序预测的效果提升。

论文标题：FREDF: LEARNING TO FORECAST IN FREQUENCY DOMAIN

下载地址：​​https://arxiv.org/pdf/2402.02399​​

开源代码：​​https://github.com/Master-PLC/FreDF​​

1.背景

在天气预报、工业维护等领域，准确的时序预测可以帮助我们做出更好的决策和规划。时间序列数据的自相关性——即不同时间点数据之间的相关性——为预测带来了独特的挑战。这种自相关性既存在于多步输入序列中，也存在于多步预测的标签序列中。

现有的时间序列预测方法主要关注输入序列中的自相关性。为了建模自相关性，各种模型结构(如RNN、CNN、GNN等)被相继提出。但大多数方法却忽略了一个关键方面：预测标签之间的自相关性：这种相关关系难以通过设计模型结构来建模，需要对预测范式进行特别设计。

特别是，时下流行的直接预测方法（Direct Forecast，DF），通过多任务方式一次性预测多步，以避免误差累积，从而提升建模精度。然而本文证明：DF假设标签序列在给定输入序列的条件下是条件独立的，从而忽略了标签序列中的自相关性。

为了绕开标签序列在时域中的自相关性，本文提出将其投影到“自相关不显著”的视图中，再用DF对投影值做模型训练和预测。例如，把标签序列投影到频域：，其中 是不同频率上的频谱分量。与时域中的自相关 不同，在频域中，频点1的频谱分量对频点2的频谱分量没有直接影响，从而对标签自相关性的影响进行了抑制。

※和现有FFT-based工作的区别：在时间序列预测领域，已经有了较多基于频域学习的工作，例如AutoFormer、FedFormer、FreTS等。这些方法主要是通过设计模型结构处理输入序列中的自相关性。相对地，FreDF使用频域变换优化预测范式，处理标签序列中的自相关性（LA）；不涉及改变模型结构以处理输入序列中的自相关性。

2.标签序列中的自相关性

LA在时域的显著性：在时间序列的生成过程中，当前时刻的预测不仅与历史数据有关，更与上一时刻的状态有关。也就是说：在给定历史数据后，不同时间步之间的标签也应该存在相关性（如蓝色箭头表示）。为验证这一假说，使用DoubleML方法量化给定历史数据后预测时间步之间的因果关系强度，结果说明：LA在真实数据中是非常显著的。

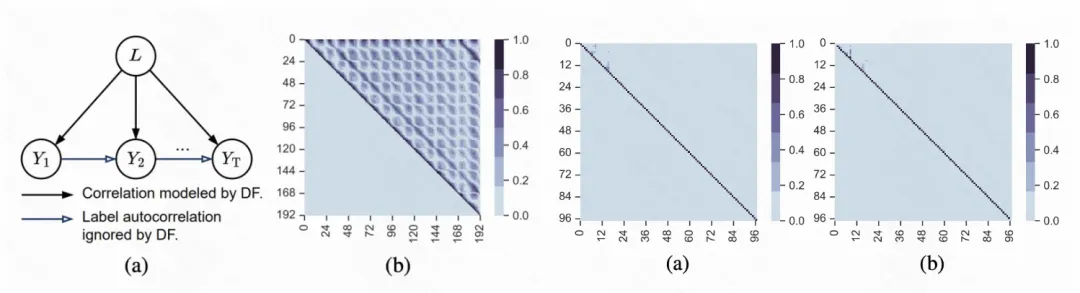
现有直接预测范式忽略了对LA的建模：直接预测（Direct Forecast，DF）范式使用一个多输出头同时预测未来多个时间步的标签值。然而，DF只是复用了一般的多任务学习方法，没有考量标签之间的依存关系（LA）。特别是，即使标签之间没有关联，也可以使用上述损失函数训练一个多任务模型。在训练模型时，DF试图最小化预测标签序列与真实标签序列之间的误差；这假设了标签序列在不同时间步之间是条件独立的，从而忽略了标签序列内部各时间步之间的相关性（LA）。

LA在频域的显著性得到抑制：为了处理LA，是不是可以对标签序列进行一定的变换，使得变换后序列的相关性得到抑制呢？对序列来说，一个很自然的方法是傅里叶变换，将序列用时域转换到频域为验证这一假说，图1（c-d）量化了给定历史数据后频域点之间的因果关系强度，发现不同频点上的频谱分量基本没有相关性。所以，将标签序列变换到频域可以有效抑制LA。

论文中进一步提供了在3个额外真实数据的验证，实验结果均展现出类似性质。

3.FreDF模型结构

FreDF 的核心思想是将预测任务从时域转换到频域。之前的验证表明，标签序列变换到频域后LA不显著，因此适配DF的条件独立性假设，所以可以使用多任务方法直接预测多个频点的频谱分量。这种方法避免了自相关性对模型的影响，且绕开了显式建模自相关性的复杂性。

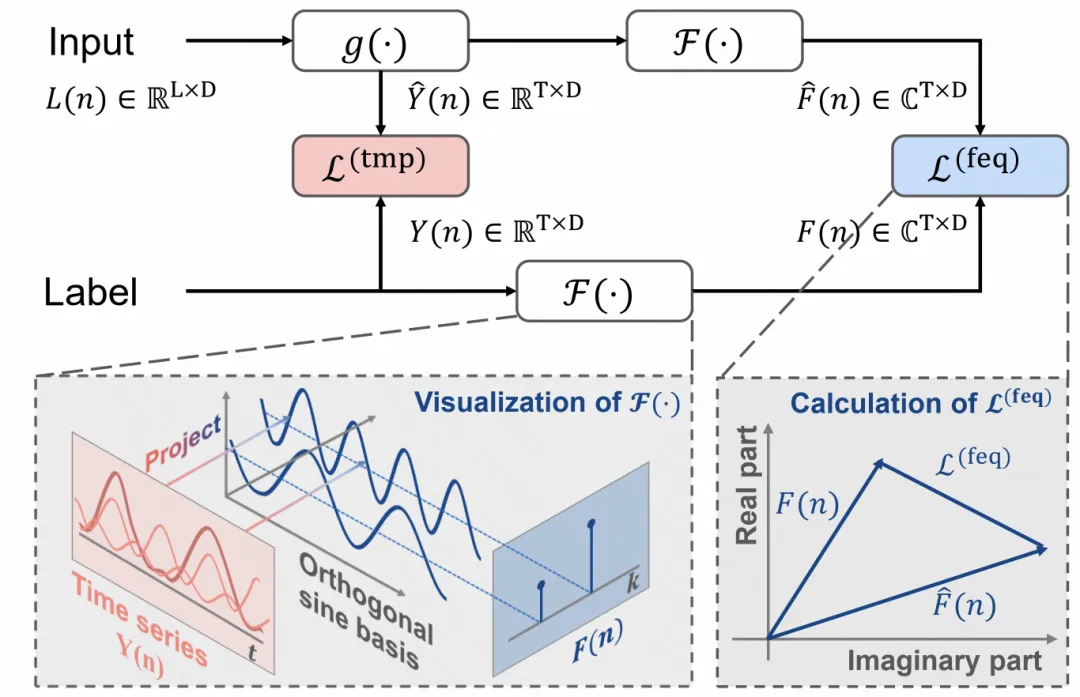
具体的实现方法如下。文中使用傅里叶变换将标签序列和预测序列都从时域转换到频域。这里和其他频域信息引入工作的区别在于，其他工作一般是将输入转换到频域，但最后还是在时域中预测。本文则是完全将数据转换到频域，预测也是在频域中进行预测的，损失函数也定义在频域中。频域损失函数如下：

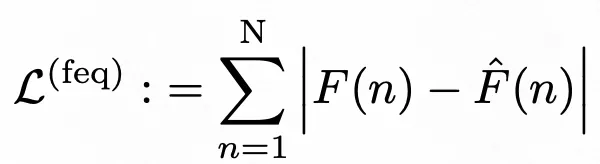
最终损失函数由时域和频域损失函数融合得到：

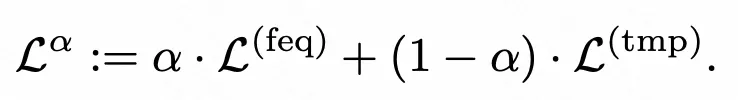
FreDF 方法不依赖于特定的预测模型或变换方法。它可以与现有的多种预测模型（Transformer、MLP）和变换方法（如用Chebyshev、Legendre变换代替FFT等）结合使用，从而提高了方法的适用性和灵活性。

4.实验效果

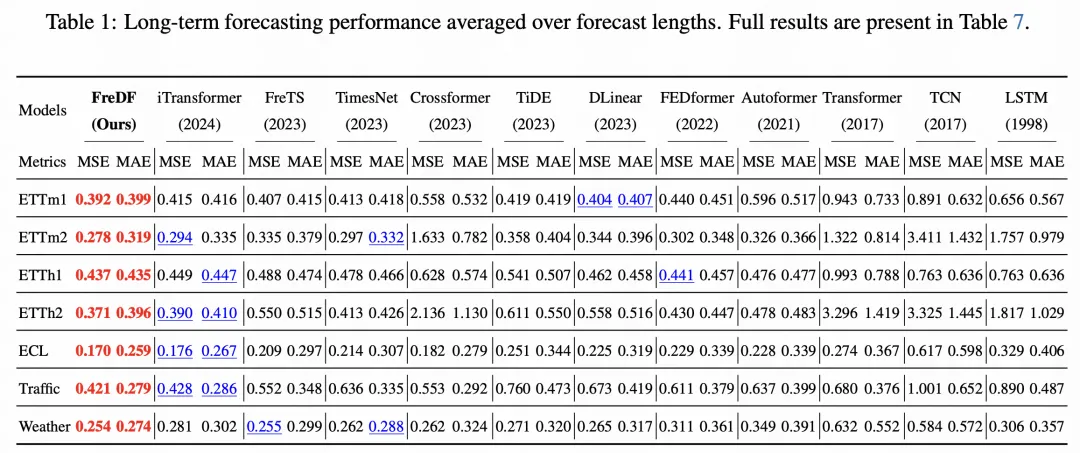
文中在长期和短期时间序列预测上均进行了实验验证。FreDF可以显著提高预测性能。以ETTm1数据集为例，FreDF将iTransformer的MSE降低了0.019,这一改进与过去1.5年中该数据集性能提升可比（Fedformer到TimesNet,MSE降低了0.017）。FreDF这一简单的改进，可以超越部分设计精巧的模型架构所能带来的性能提升。在部分数据集上，它将iTransformer的性能提升到了超过了一些原本优于iTransformer的模型：ETT、Weather。

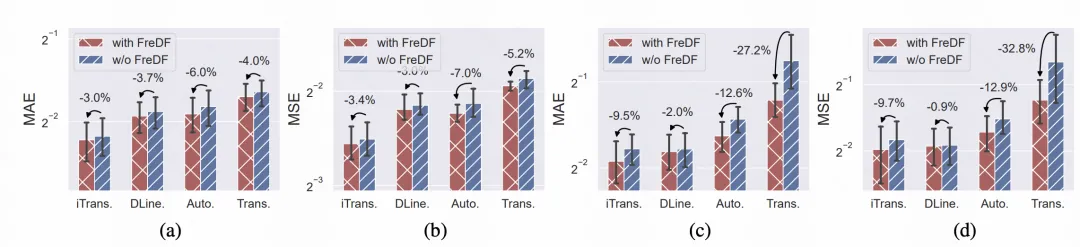
论文还测试了FreDF在不同神经网络架构上的表现，包括iTransformer、DLinear、Autoformer和Transformer等，以证明其与模型无关的特性：可以切实有效提升大多数主流时序预测模型的精度。

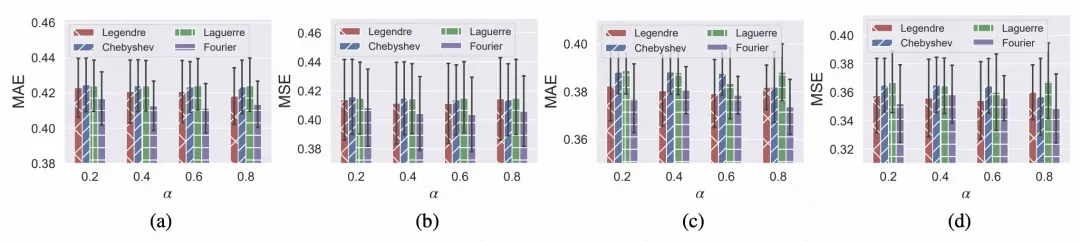
论文进一步测试了FreDF使用不同变换方案的性能表现，包括广义FFT方法（沿时间维度的1dFFT、沿变量维度的1dFFT、时间-变量维度的2dFFT）和正交基投影方法（勒让德基、拉盖尔基、切比雪夫基、傅里叶基），也有一些很有趣的发现和讨论；具体请参考论文原文。

本文转载自 ​​圆圆的算法笔记​​，作者： Fareise